# 一、Fibonacci 博弈
# 描述
基本的斐波那契博弈(Fibonacci Game)描述如下:
有一堆石子,两个顶尖聪明的人玩游戏,先取者可以取走任意多个,但不能全取完,之后每次可以取的石子数至少为 1,至多为对手刚取的石子数的 2 倍。约定取走最后一个石子的人为赢家,求必败态。
# 结论
当且仅当总石子数为斐波那契数时,先手必败。
# 证明
证明如下,转自大佬证明
用到了 Zeckendorf 定理(齐肯多夫定理):任何正整数可以表示为若干个不连续的 Fibonacci 数之和。
# 二、Bash 博弈
# 描述
基本的巴什博弈(Bash Game)描述如下:
有一堆 n 个物品,两人轮流取走物品,每次至少取一个,最多取 m 个,最后取光者获胜。
# 结论
若 n % (m+1) == 0,则先手必败
bool FirstWin(int n, int m) { // 先手必胜返回 true | |
return n % (m+1) != 0; | |
} |
# 证明
博弈过程如下:证明
这里简单说说
同余定理:若 n%(m+1) = r, 若先取者拿走 r 个,后者无论拿走 1~m 任意个,先手都可以再拿走若干个凑够(m+1)个,则先手必赢。反之先手必败。当 n<m 时,先手可以一次取完,也是必胜
# 巴什博弈变形
有一堆 n 个物品,两人轮流取走物品,每次至少取 p 个,最多取 q 个,剩余不足 p 个时一次取完,最后取光者胜利。
若 n%(p+q) = r, 则当 r != 0 && r < p 时先手必胜,反之先手必败
# 三、Wythoff 博弈
# 描述
基本的威佐夫博弈(Wythoff Game)描述如下:
有两堆各若干个物品,两个人轮流从某一堆或同时从两堆中取同样多的物品,每次至少取一个,多者不限,最后取光者得胜。
# 结论
设两堆物品各有 a、b 个,求出 ab 的差值后乘以黄金分割比,看结果是否等于 ab 中的最小值,若等于则先手必败
bool FirstWin(int a, int b) { // 先手必胜返回 true | |
double G = (sqrt(5.0)+1) / 2; // 黄金分割比 | |
int t = abs(a-b) * G; | |
return d != min(a,b); | |
} |
# 证明
证明较复杂… 暂存一下板子,这里看证明
# 四、Nim 博弈
# 描述
基本的尼姆博弈(Nim Game)描述如下:
有若干堆各若干个物品,两个人轮流从某一堆取任意多的物品,每次至少取一个,多者不限,最后取光者得胜。
# 结论
将 N 堆物品数量全部异或后,若结果为 0 则先手必败,否则先手必胜
bool FirstWin(int a, int b) { // 先手必胜返回 true | |
int ans = 0; | |
for(int i = 0; i < N; ++i) ans ^= a[i];//a [i] 为物品数量 | |
return ans != 0; | |
} |
# 证明
证明也很复杂… 这里看证明
后面会介绍 SG 函数,一般将最终局面的 SG 值设为 0
SG 定理:游戏的和的 SG 值是各个子游戏的 SG 值的异或。
知道了以上结论,想到 Nim 游戏实际上可以分为 n 个 Bash 游戏,而 Bash 游戏若可以无限取子,则以当前局面剩余石子数为状态,SG (x)=x。所以这个题目的答案即为各个堆石子数的异或值,若值为 0,先手必败,否则先手总有方案使得下一局面异或值为 0,后手必败。
# 变形
参考博客 Nim 博弈及其变形
# 反 Nim 博弈
反尼姆博弈顾名思义,
有若干堆各若干个物品,两个人轮流从某一堆取任意多的物品,每次至少取一个,多者不限,最后取光者失败。
例题 E - Misere Nim
先手只有两种情况必胜,1 是所有堆石子数全为 1,且异或和为 0,2 是有石子数不为 1 的堆,且异或和不为 0
# 五、SG 函数
参考博客:SG 函数、组合游戏 - SG 函数和 SG 定理
# 1. 概念介绍
# ICG 博弈游戏(公平组合游戏)
条件如下: 题目描述一般为 A,B 两人做游戏
- A、B 交替进行操作
- 每操作一次,选手可以在合法操作集合中任选一种操作。
- 对于游戏的任何一种可能的局面,合法的操作集合只取决于这个局面本身,不取决于其它因素(跟选手,以前的所有操作无关)
- 如果当前选手无法进行合法的操作,判负
以上面所提的巴什博弈做背景,有一堆 n 个物品,两人轮流取走物品,每次至少取一个,最多取 m 个,最后取光者获胜。
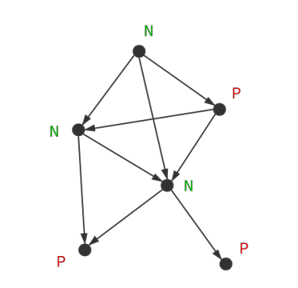
一个公平游戏可以抽象地用一个有向无环图来表示,这个图中每个点都对应一个状态,每条有向边代表从一个状态到另一个状态的合法操作。
# 必胜态与必败态
- 必败态(P-position):上一个选手(即刚操作完的选手)处于必胜局面,此时谁面临此状态谁必败。
- 必胜态(N-position):下一个选手(即将操作的选手)处于必胜局面,此时谁面临此状态谁必胜。
性质:
- 所有的终结点都是必败态
- 从任何必胜态操作,至少能有一种方式进入必败态
- 无论如何操作, 从必败态都只能进入必胜态
# 2.SG 函数
# 定义 mex 运算
先定义 mex (minimal excludant) 运算,这是施加于一个集合的运算,表示最小的不属于这个集合的非负整数。
- 如 mex {2,3,5}=0、mex {0,1,2,4}=3、mex {}=0。
对于任意状态 x,定义 SG (x)=mex (S),其中 S 是 x 后继状态的 SG 函数值的集合。如 x 有三个后继状态分别为 a、b、c,那么 SG (x)=mex {SG (a), SG (b), SG (c)}。 这样,集合 S 的终态必然是空集,所以当且仅当 x 为必败点 P 时,SG 函数的终态为 SG (x)=0。
通过 SG 函数,每个 ICG 都可以转换成 Nim 博弈。SG 函数的定义域为 ICG 的决策树上的所有节点,此时具体定义为:SG (x)=mex {SG (y)|y 是 x 的节点}。对于 ICG 的决策树上的节点 u,我们可以把它想象成一个只有一堆石子,个数为 SG (u) 的 Nim 博弈。SG 函数的求解方式我是通过这个博客理解的: 组合游戏 - SG 函数和 SG 定理。
取石子问题
有 1 堆 n 个的石子,每次只能取 {1, 3, 4} 个石子,先取完石子者胜利,那么各个数的 SG 值为多少?
SG[0]=0,f[]={1,3,4},
- x=1 时,可以取走 1 - f {1} 个石子,剩余 {0} 个,所以 SG [1] = mex { SG [0] }= mex {0} = 1;
- x=2 时,可以取走 2 - f {1} 个石子,剩余 {1} 个,所以 SG [2] = mex { SG [1] }= mex {1} = 0;
- x=3 时,可以取走 3 - f {1,3} 个石子,剩余 {2,0} 个,所以 SG [3] = mex {SG [2],SG [0]} = mex {0,0} =1;
- x=4 时,可以取走 4- f {1,3,4} 个石子,剩余 {3,1,0} 个,所以 SG [4] = mex {SG [3],SG [1],SG [0]} = mex {1,1,0} = 2;
- x=5 时,可以取走 5 - f {1,3,4} 个石子,剩余 {4,2,1} 个,所以 SG [5] = mex {SG [4],SG [2],SG [1]} =mex {2,0,1} = 3;
以此类推…
x = 0 1 2 3 4 5 6 7 8…
SG[x] = 0 1 0 1 2 3 2 0 1…
由上述实例我们就可以得到 SG 函数值求解步骤,那么计算 1~n 的 SG 函数值步骤如下:
- 使用数组 f 将可改变当前状态的方式记录下来。
- 用另一个数组将当前状态 x 的后继状态标记。
- 最后模拟 mex 运算,也就是我们在标记值中 搜索 未被标记值 的最小值,将其赋值给 SG (x)。
- 不断的重复 2 - 3 的步骤,就完成了 计算 1~n 的函数值。
模板如下:
//f [N]: 可改变当前状态的方式,N 为方式的种类,f [N] 要在 getSG 之前先预处理 | |
//SG []:0~n 的 SG 函数值 | |
//S []: 为 x 后继状态的集合 | |
int f[N],SG[MAXN],S[MAXN]; | |
void getSG(int n){ | |
int i,j; | |
memset(SG,0,sizeof(SG)); | |
// 因为 SG [0] 始终等于 0,所以 i 从 1 开始 | |
for(i = 1; i <= n; i++){ | |
// 每一次都要将上一状态 的 后继集合 重置 | |
memset(S,0,sizeof(S)); | |
for(j = 0; f[j] <= i && j <= N; j++) | |
S[SG[i-f[j]]] = 1; // 将后继状态的 SG 函数值进行标记 | |
for(j = 0;; j++) if(!S[j]){ // 查询当前后继状态 SG 值中最小的非零值 | |
SG[i] = j; | |
break; | |
} | |
} | |
} |
# 3.SG 定理
- 游戏和的 SG 函数是所有子游戏的 SG 函数的异或和,其中所有子游戏互相独立。
- 所以当且仅当每堆石子的 SG 函数的异或和不为 0 时,先手必胜。
# 六、Green Hackenbush(树上删边游戏)
做题第一题就被卡住了,搜了下题解发现是没学过的 Green 博弈
参考博客:博弈 - Green Hackenbush,以下内容都是这里面的
# 1.Hackenbush 游戏概述
Hackenbush 游戏是通过移除一个有根图的某些边,直到没有与地板的相连的边。地板用虚线来表示,其中移除某一条边的时候,那条边以上所连着的所有边都会移除,就像砍树枝那样,树枝以上的部分也会被移除。在这里,我们讨论这个游戏的公平版本,每个玩家在他的回合可以删除任意的边。这个版本叫做 Green Hackenbush,每条边都是绿色的,下面我们简称 GH 游戏。这里还有一个不公平版本,叫做 Blue-Red Hackenbush,有些边是蓝色,有些边是红色,而玩家一只能删除蓝色边,玩家二只能删除红色边。总的来说,Hackenbush 游戏,可能会有只供玩家一删除的蓝色边,只供玩家二删除的红色边,还有两个玩家都可以进行操作的绿色边。
# 2. 克朗原理(Colon Principle)
对于树上的某一个点,它的分支可以转化成以这个点为根的一根竹子,这个竹子的长度就是它各个分支的边的数量的异或和
所有边权值为 1,则是裸的 green 博弈,每个点的 sg 函数 = 子节点的 sg 函数 + 1 的异或和。
权值不同时,当 AB 权值 = 1 时,sg [A]=sg [B]+1。
当 AB 权值为偶数时,sg [A]=sg [B]。
当 AB 权值为奇数时,sg [A]=sg [B]^1