首页 笔记 数据结构

# 一、拓扑排序

# 1. 概念定义

# AOV 网络

例如，假定一个计算机专业的学生必须完成图 3-4 所列出的全部课程。从图中可以清楚地看出各课程之间的先修和后续的关系。如课程 C5 的先修课为 C2，后续课程为 C4 和 C6。通常，我们把这种顶点表示活动、边表示活动间先后关系的有向图称做顶点活动网 (Activity On Vertex network)，简称 AOV 网。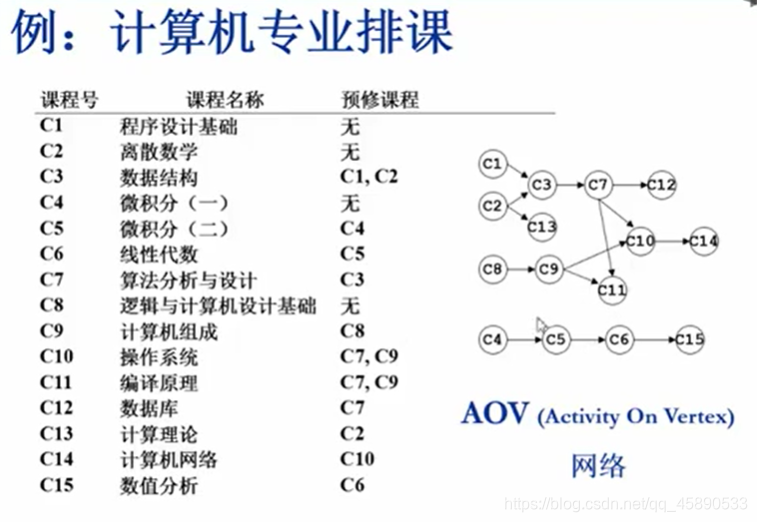
以计算机

# 拓扑序、DAG

  • 若图中从 V 到 W 有一条有向路径，则 V 一定排在 W 之前。满足该条件的顶点序列称为一个拓扑序
  • 获得一个拓扑序的过程就是拓扑排序
  • AOV 若有合理的拓扑序，则必定是有向无环图（Directed Acyclic Graph,DAG）

# 2. 拓扑排序思路

拓扑排序的思路是每次都找一个入度为 0 的顶点并输出，并且将该顶点所有邻接点入度减 1。
可以看出，找入度为 0 的顶点是关键，若每次都要遍历那必定会耗费大量时间空间，所以更聪明的算法是，随时将入度变为 0 的顶点放入一个容器中。
伪码描述如下

void TopSort() {
 int cnt = 0;
    for(图中的每个顶点V) 
  if( Indegree[W] == 0)
   Enqueue(V,Q);
 while(!isEmpty(Q)) {
  V = Dequeue(Q);
  输出V,或记录V的输出序号,cnt++;
        for(V的每个邻接点W)
         if(--Indegree[W] == 0)
             Enqueue(V,Q);
 }
 if(cnt != |V|)
  Error("图中有回路");
}

模板代码：

const int maxn = 1005;
int N,M;// 顶点数、边数（活动数）
int edge[maxn][maxn];
int mint[maxn];// 到每个活动检查点的最短时间
int In[maxn];// 每个活动检查点的入度
void init() {
    memset(edge, -1, sizeof(edge));
    memset(mint, 0, sizeof(mint));
    memset(In, 0, sizeof(In));
}
bool Topsort() {// 拓扑排序
    queue<int> q;
    for(int i = 0; i < N; ++i) {
        if(In[i] == 0) 
            q.push(i);
    }
    int cnt = 0;
    while(!q.empty()) {
        int v = q.front();
        q.pop();
        cnt++;
        for(int i = 0; i < N; ++i) {
            if(v == i || edge[v][i] == -1) continue;// 检查以 v 为起点的所有边
            In[i]--;
            // 其他操作
            if(In[i] == 0) q.push(i);
        }
    }
    if(cnt != N) return false;
    else return true;
}

# 例题

08 - 图 8 How Long Does It Take (25 分)
是一道拓扑排序的变形，程序不算复杂，建议尝试；
题意、代码及思路指路博客：

# 3. 解决实际问题

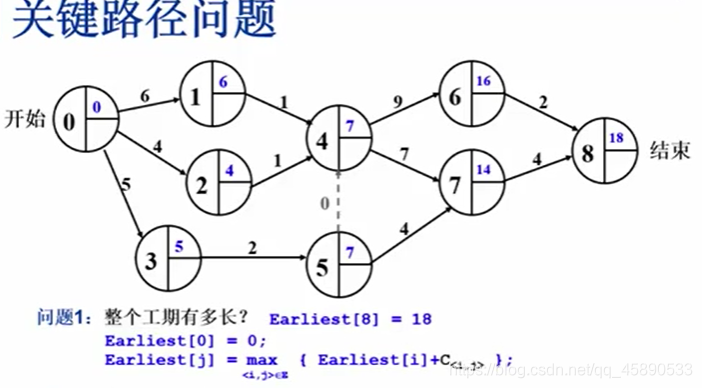
# 关键路径问题

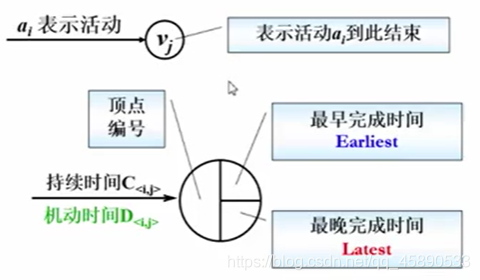
# AOE 网络 (Activity On Edge) 网络

  • 一般用于安排项目的工序
  • 在 AOE 网络中，活动是表示在边上的，顶点被分为三个部分：顶点编号、最早完成时间和最晚完成时间
    https://www.icourse163.org/learn/ZJU-93001?tid=1459700443#/learn/content?type=detail&id=1235254066&cid=1254945243&replay=true
# 先推出最早完成时间 —— mint [j] = max ( mint [ j ], mint [ i ]+edge [ i ][ j ])

在这里插入图片描述

# 再由后往前推出最晚完工时间 —— maxt [i] = min ( maxt [ j ], maxt [ j ]-edge [ i ][ j ])
# 即可得机动时间 —— D [i][ j ] = maxt [ j ] - mint [ i ] - edge [ i ][ j ]

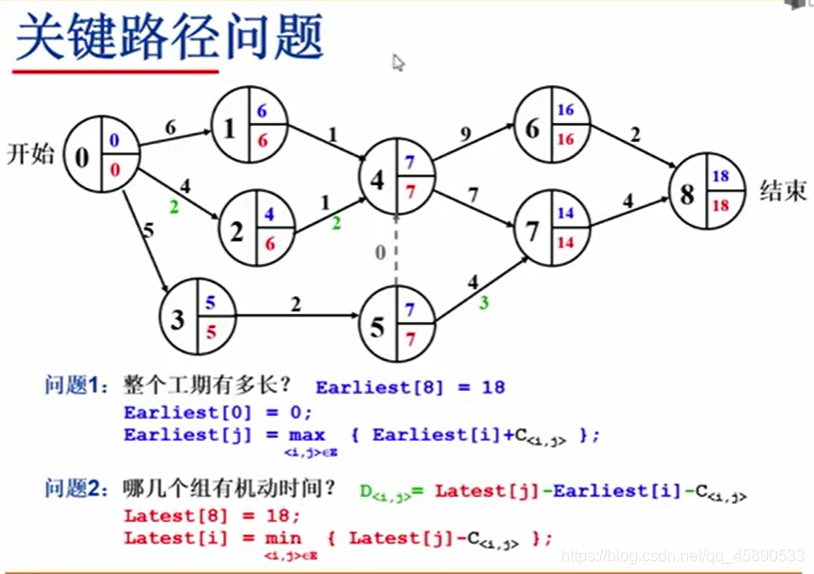
在这里插入图片描述
而关键路径，是由绝对不允许延误的活动组成的路径，即没有机动时间的路径。

# 例题

08 - 图 8 How Long Does It Take (25 分)
是一道拓扑排序的变形，求最早完成时间
08 - 图 9 关键活动 (30 分)
求关键路径
代码及思路指路博客：PTA 数据结构题目集 第八周 —— 图（下）

# 二、简单排序

# 1. 前提

void X_Sort(ElementType A[], int N);
  • 为简单起见，讨论整数的从小到大排序
  • N 为正整数
  • 只讨论基于比较的排序（> = < 有定义）
  • 只讨论内部排序
  • 稳定性：任意两个相等的数据排序前后的相对位置不发生改变
  • 没有哪一种排序是任何情况下都表现最好的！

# 2. 排序算法

测试题目：09 - 排序 1 排序 (25 分)

# 冒泡排序

它重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序（如从大到小、首字母从 Z 到 A）错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。
这个算法的名字由来是因为越小的元素会经由交换慢慢 “浮” 到数列的顶端（升序或降序排列），就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样，故名 “冒泡排序”。
<p align="right">—— 摘自百度百科 </p>

void Bubble_Sort(ll a[], int N) {
    for(int P = N-1; P >= 0; P--) {
        bool flag = false;
        // 一趟冒泡 从上往下比较，上边大于下边则交换
        for(int i = 0; i < P; ++i) {    
            if(a[i] > a[i+1]) {
                swap(a[i], a[i+1]);
                flag = true;
            }
        }
        if(!flag) break; // 一趟下来已经有序了，未发生交换
    }
}

# 时间复杂度

最好情况：顺序，时间复杂度 T = O (N)
最坏情况：整个逆序，时间复杂度 T = O (N2)

# 优缺点

优点：简单易写，只需交换相邻元素，即使是单向链表也可直接排序，稳定（交换前后相等元素的位置不变）
缺点：时间复杂度较大，慢！

# 测试结果

测试结果如下，有 3 个样例没过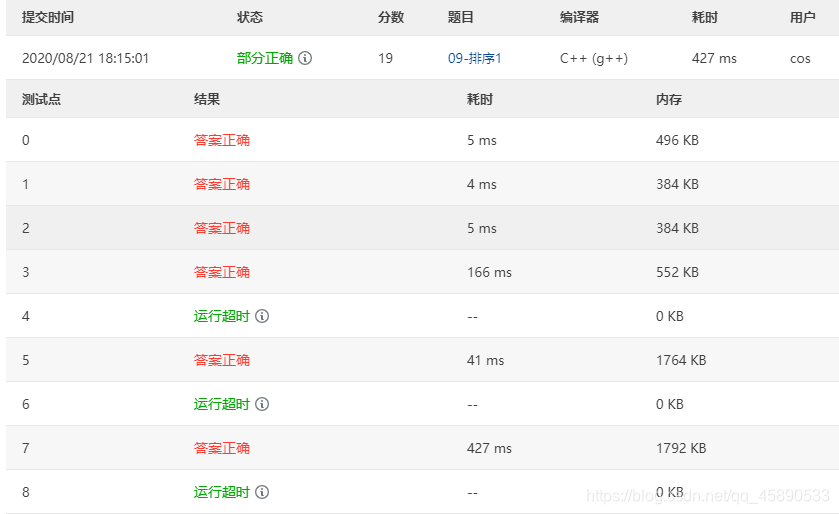
在这里插入图片描述

# 插入排序

插入排序，一般也被称为直接插入排序。对于少量元素的排序，它是一个有效的算法。插入排序是一种最简单的排序方法，它的基本思想是将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增 1 的有序表。在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动。
<p align="right">—— 摘自百度百科 </p>

void Insertion_Sort(ll a[], int N) {
    for(int P = 1; P < N; P++) {
        ll t = a[P];// 摸下一张牌
        int i;
        for(i = P; i > 0 && a[i-1] > t; --i) 
            a[i] = a[i-1];  // 移出空位 直到前面那个这个元素小于当前元素
        a[i] = t;   // 新牌落位
    }
}

# 时间复杂度

最好情况：顺序，时间复杂度 T = O (N)
最坏情况：整个逆序，时间复杂度 T = O (N2)
一般情况下时间复杂度下界计算：
交换两个相邻元素正好消去 1 个逆序对
设有 I 个逆序对
则 T (N,I) = O (N+I)

# 优缺点

优点：稳定
缺点：比较次数不一定，比较次数越少，插入点后的数据移动越多，尤其是当数据总量庞大的时候

# 测试结果

测试结果如下，挺给力的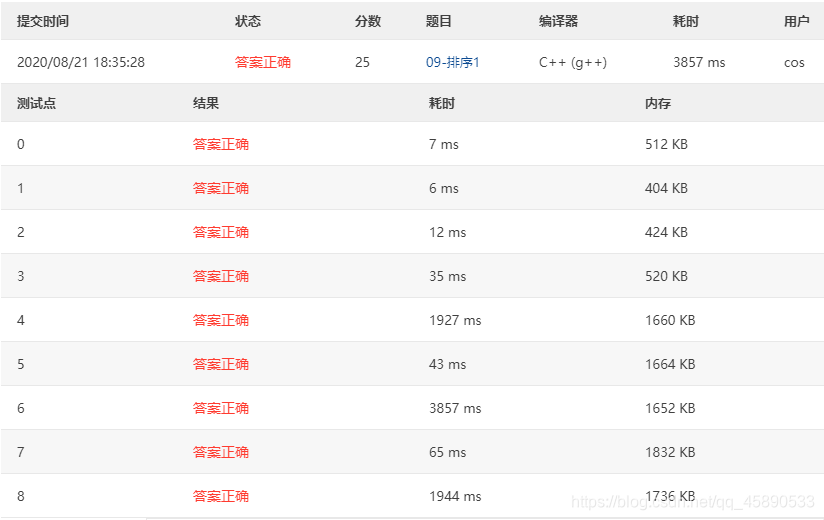
在这里插入图片描述

# 如何提高效率

有定理如下

  • 任意 N 个不同元素组成的序列平均具有 N (N-1)/4 个逆序对
  • 任何仅以交换相邻两元素来排序的算法，其平均时间复杂度为 O (N2)

所以要提高算法效率，我们必须

  • 每次消去不止 1 个逆序对！
  • 每次交换相隔较远的 2 个元素！

# 希尔排序

利用了插入排序的简单，克服插入排序只能交换相邻两元素的缺点。

希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个文件恰被分成一组，算法便终止。
<p align="right">—— 摘自百度百科 </p>
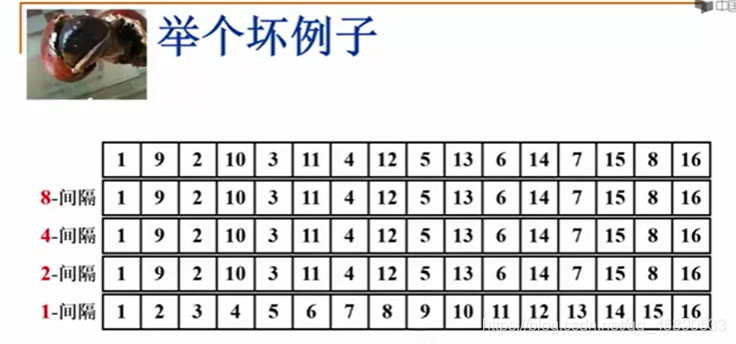
定义增量序列 DM >DM-1>…>D1 = 1
对每个 Dk 进行 “Dk 间隔” 排序（k=M，M-1，……，1）
<font color="#dd0000"> 注意:“Dk 间隔” 有序的序列，在执行 “Dk-1 间隔” 排序后，仍然是 “Dk 间隔” 有序的！</font>

# 希尔增量序列选取

  • 原始希尔排序增量序列 DM = N/2， Dk = Dk+1 / 2
    • 增量元素不互质，则小增量可能根本不起作用！
      在这里插入图片描述
void Shell_Sort(ll a[], int N) {
    for(int D = N/2; D > 0; D /= 2) { // 希尔增量序列
        for(int P = D; P < N; ++P) { // 插入排序
            ll t = a[P];
            int i;
            for(i = P; i >= D && a[i-D] > t; i -= D) 
                a[i] = a[i-D];
            a[i] = t;
        }
    }
}
  • Hibbard 增量序列
    • Dk = 2k-1 —— 相邻元素互质
  • Sedgewick 增量序列等

# 优缺点

优点：快，数据移动少！适用于数据量较大的情况
缺点：不同的增量序列选取会导致算法复杂度差异，如何选取增量序列只能根据经验，不稳定

# 测试结果

可以看到耗时都没超过 100ms，在这些测试样例里的速度还是很理想的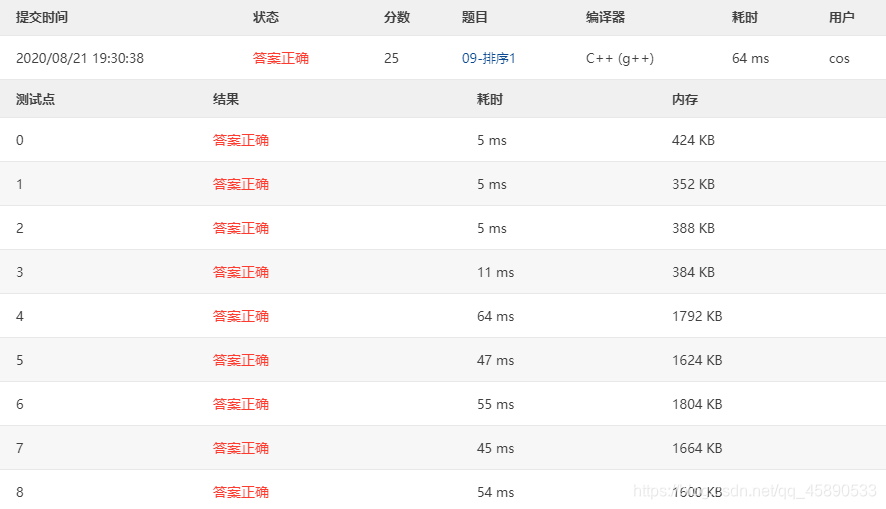
在这里插入图片描述

# 选择排序

在介绍堆排序前，先介绍选择排序，老朋友了

void Selection_Sort(ll a[], int N) {
    for(int i = 0; i < N; ++i) {
        int mini = 0;
        ll ans = inf;
        // 找 i 后边的最小元 并将其位置赋给 mini
        for(int j = i; j <= N-1; ++j) {
            if(a[j] < ans) {
                ans = a[j];
                mini = j;
            }
        }
        // 将未排序部分的最小元换到有序部分的最后位置
        swap(a[i], a[mini]);
    }
}

# 时间复杂度

无论如何复杂度都为 O (N2)

# 测试结果

测试结果如下，虽然都能过，但后几个样例耗时都很大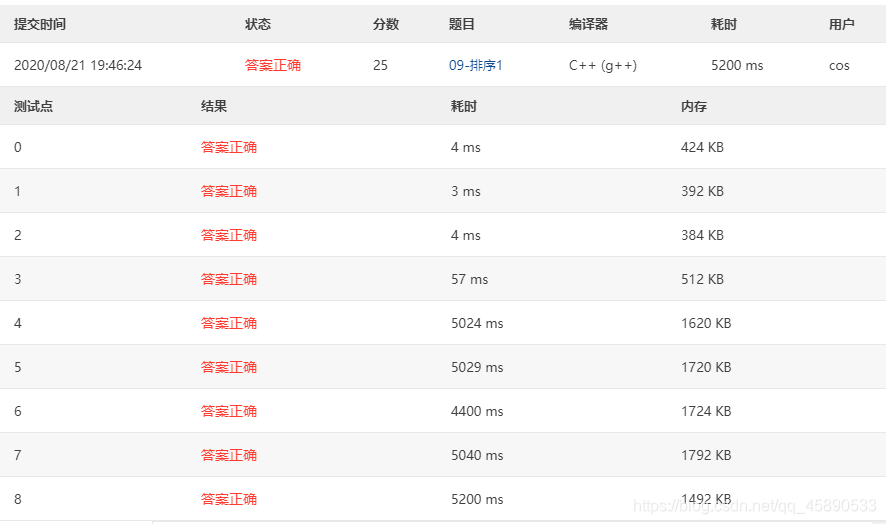
在这里插入图片描述

# 堆排序

这里以排成升序为例，我们需要将其原始数组调整成下标从 0 开始的最大堆，再将最大堆顶与当前最后的元素交换（相当于删除最大堆顶）后调整

void swap(ll& x, ll& y) {
    ll t = x;
    x = y;
    y = t;
}
void PercDown(ll a[], int N, int rt) {
    // 将 N 个元素的数组中以 a [now] 为根的子堆调整为最大堆
    int father, son;
    ll tmp = a[rt];
    for(father = rt; (father*2+1) < N; father = son) {
        son = father * 2 + 1;// 左儿子
        if(son != N-1 && a[son] < a[son+1]) // 右儿子存在且比左儿子大
            son++;
        if(tmp >= a[son]) break;// 找到该放的地方
        else a[father] = a[son];// 下滤
    }
    a[father] = tmp;
}
inline void BuildHeap(ll a[], int N) {
    for(int i = N/2-1; i >= 0; --i) {
        PercDown(a, N, i);
    }
}
void Heap_Sort(ll a[], int N) {
    BuildHeap(a, N);
    for(int i = N-1; i > 0; --i) {
        swap(a[0], a[i]);// 最大堆顶 a [0] 与 a [i] 交换
        PercDown(a, i, 0);// 删除后进行调整
    }
}

# 时间复杂度

堆排序给出了最佳的平均时间复杂度
最好情况 O (nlogn)
最坏情况 O (nlogn)
平均时间复杂度 O (nlogn)

# 优缺点

优点：快！即使是最坏情况下性能也很优越，使用的辅助空间少
缺点：不稳定，不适合对象的排序。

# 测试结果

测试结果如下，好像比希尔排序给力些哦～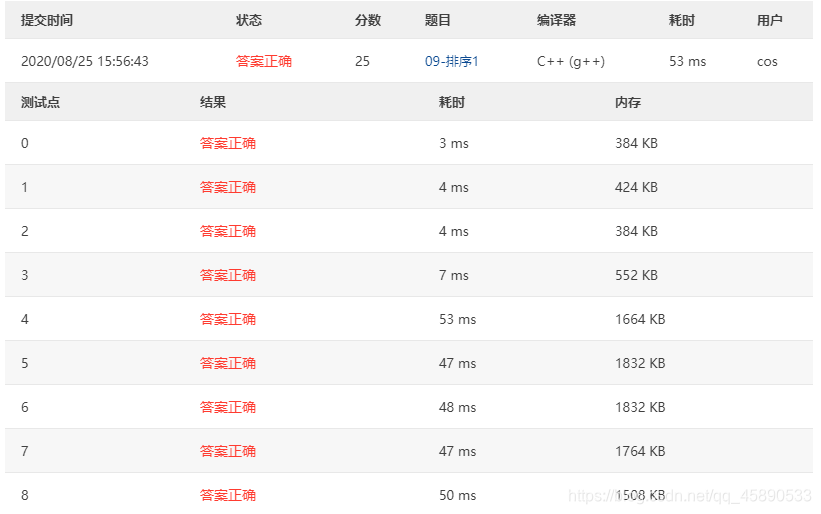
在这里插入图片描述

# 归并排序

核心是有序子列的合并，这里给出递归实现的版本～非递归实现看这里哦归并排序循环实现

void Merge(ll a[], int s, int m, int e, ll tmp[]) {
    // 将数组 a 的局部 a [s,m] 和 a [m+1,e] 合并到数组 tmp, 并保证 tmp 有序
    // 然后再拷贝回 a [s,m]  时间复杂度 O (e-m+1), 即 O (n);
    int pb = s;//pb 为 tmp 数组的下标
    int p1 = s, p2 = m+1;//p1 指向前一半 p2 指向后一半
    while (p1 <= m && p2 <= e) {
        if (a[p1] < a[p2])
            tmp[pb++] = a[p1++];
        else 
            tmp[pb++] = a[p2++];
    }
    while(p1 <= m) 
        tmp[pb++] = a[p1++];
    while(p2 <= e) 
        tmp[pb++] = a[p2++];
    for (int i = 0; i < e-s+1; ++i)
        a[s+i] = tmp[i];
}
void MergeSort(ll a[], int s, int e, ll tmp[]) {
    if (s < e) {// 若 s>=e 则不做任何事情
        int m = s + (e-s)/2;
        MergeSort(a, s, m, tmp);// 前一半排序
        MergeSort(a, m+1, e, tmp);// 后一半排序
        Merge(a, s, m, e, tmp);// 归并 将 a 中 s 到 m 和 m+1 到 e 的两个数组有序的归并
    }
}

# 时间复杂度

最好情况 O (nlogn)
最坏情况 O (nlogn)
平均时间复杂度 O (nlogn)

# 优缺点

优点：稳定、快
缺点：较占用空间

# 测试结果

测试结果如下，你品，你细品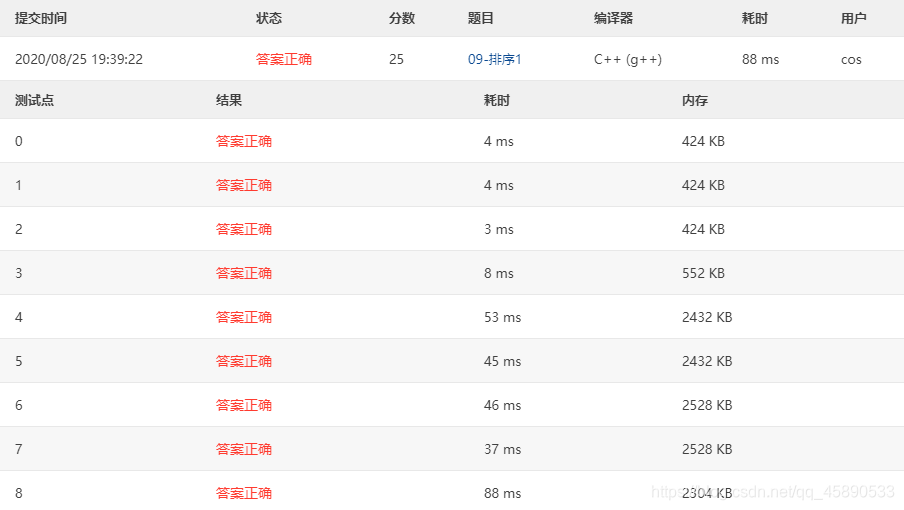
在这里插入图片描述

# 快速排序

1. 设 k = a [0], 将 k 挪到适当位置，使得比 k 小的元素都在 k 左边，比 k 大的元素都在 k 右边 (在 O (n) 时间完成)
2. 把 k 左边的部分快速排序
3. 把 k 右边的部分快速排序
k 为主元

void QuickSort(ll a[], int s, int e){// 将 a [s,e] 快排
    if (s >= e)
        return;
    int k = a[s];
    int i = s,j = e;
    while (i != j) {
        while (j > i && a[j] >= k)  --j;
        swap(a[i],a[j]);
        while (i < j && a[i] <= k)  ++i;
        swap(a[i],a[j]);
    }// 处理完后 a [i] = k;
    QuickSort(a, s, i-1);// 快排左边部分
    QuickSort(a, i+1, e);// 快排右边部分
}

# 时间复杂度

最好情况每次正好中分 O (nlogn)
最坏情况 O (N2)
平均时间复杂度 O (nlogn)

# 优缺点

优点：是所有内部排序的最快的算法
缺点：不稳定，最坏情况下效率较慢！

# 测试结果

测试结果如下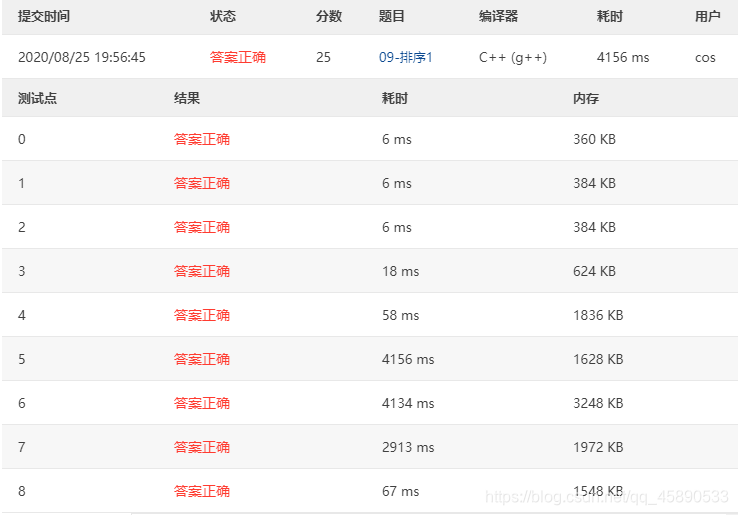
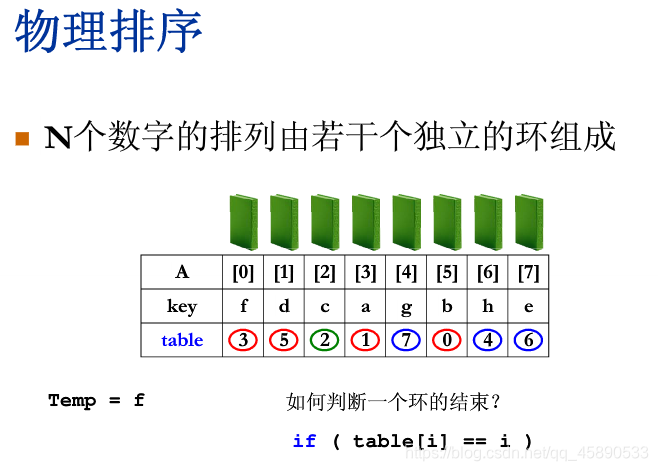
在这里插入图片描述

# 表排序

当数据量大且待排序的元素为对象、移动所需时间特别高时，我们需要间接排序
定义一个指针数组作为 “表”（table），记录待排元素
在这里插入图片描述

# 时间复杂度

最好情况初始即有序
最坏情况有 N/2 个环，每个环包含 2 个元素，交换两个元素需要走三步，需要 3N/2 次元素移动
T = O (m N)，m 是每个 A 元素的复制时间

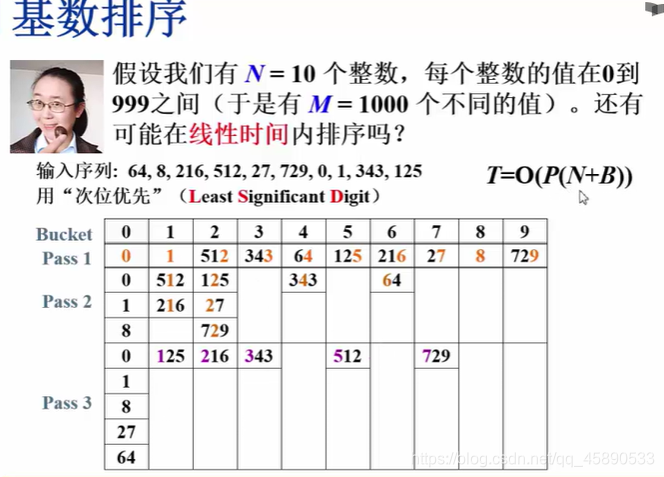
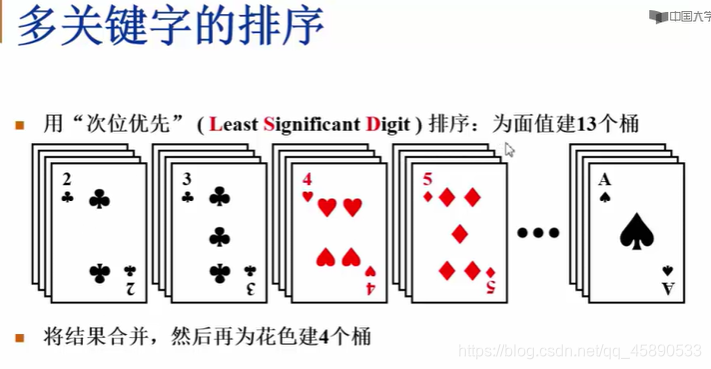
# 基数排序（桶排序的推广）

之前讲的算法都需要比较，最坏情况下也都有 Nlogn，还能更快吗？
假设我们有 N 个学生，他们的成绩是 0~100 之间的整数（于是有 M = 101 个不同的成绩值），如何在线性时间内将学生按成绩排序
LSD 主位优先 MSD 次位优先在这里插入图片描述
在这里插入图片描述

基数排序的代码我参考了这篇博客的，用的方法非常巧妙：基数排序

ll getMax(ll a[], int n) {// 找 n 个元素的 a 数组中最大数
    int maxx = a[0];
    for(int i = 1; i < n; ++i) {
        if(a[i] > maxx) maxx = a[i];
    }
    return maxx;
}
void radixsort(ll a[], int n, int exp) { // 对 n 个元素的数组 a 按照 "某个位数" 进行排序 (桶排序), 基数为 10
    ll tmp[maxn];
    ll T[20] = {0}; // 有负数的十进制 二十个桶
    for(int i = 0; i < n; ++i) //T 存储该桶里有多少个数
        T[(a[i]/exp)%10 + 10]++;
    for(int i = 1; i < 20; ++i) // 让 T 的值是在 tmp 中的位置
        T[i] += T[i-1];
    for(int i = n - 1; i >= 0; --i) {
        int now = T[(a[i]/exp)%10 + 10];// 当前这个数所应在的位置
        tmp[now-1] = a[i];
        T[(a[i]/exp)%10 + 10]--;
    }
    for(int i = 0; i < n; ++i)
        a[i] = tmp[i]; // 将排好序的 tmp 赋给 a
}
void Radix_Sort(ll a[], int n) {
    ll maxnum = getMax(a, n);
    for(int exp = 1; maxnum/exp > 0; exp *= 10) 
        radixsort(a, n, exp);
}

# 时间复杂度

N 为待排序元素个数，而 B 是桶数
O (P (N+B)) 一趟分配时间为 O (N)，一趟收集时间复杂度为 O (B)，共进行 P 趟分配和收集

# 优缺点

优点：适用于位数不多，待排序列最大位数不是特别大的情况，快
缺点：空间换时间

# 测试结果

测试结果如下，超快的说～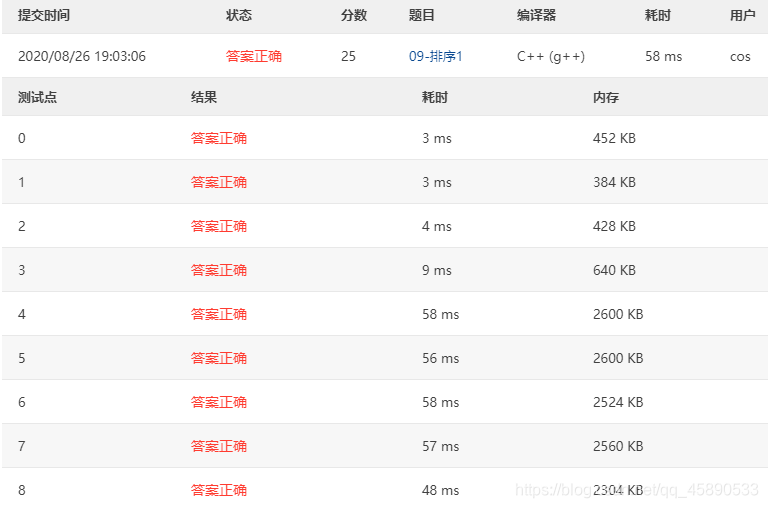
在这里插入图片描述

# 三、排序算法的比较

在这里插入图片描述

更新于 阅读次数 次

请我喝[茶]~(￣▽￣)~*

cos 微信支付

微信支付

cos 支付宝

支付宝