day14 题目:剑指 Offer 12. 矩阵中的路径、剑指 Offer 13. 机器人的运动范围
知识点:数组、回溯、搜索,难度为中等、中等
学习计划链接:「剑指 Offer」 - 学习计划
| 题目 | 知识点 | 难度 |
|---|---|---|
| 剑指 Offer 12. 矩阵中的路径 | 数组、回溯、矩阵 | 中等 |
| 剑指 Offer 13. 机器人的运动范围 | 深度优先搜索、广度优先搜索 | 中等 |
# 剑指 Offer 12. 矩阵中的路径
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中 “相邻” 单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
例如,在下面的 3×4 的矩阵中包含单词 "ABCCED"(单词中的字母已标出)。
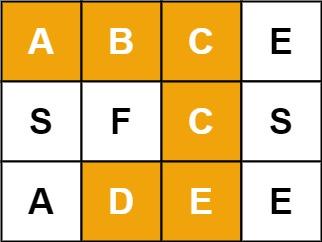
示例 1:
输入: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出: true
示例 2:
输入: board = [["a","b"],["c","d"]], word = "abcd"
输出: false
提示:
1 <= board.length <= 2001 <= board[i].length <= 200board和word仅由大小写英文字母组成
注意: 本题与主站 79 题相同:https://leetcode-cn.com/problems/word-search/
# 思路
非常典型的深搜典型题,以矩阵中每个符合单词开头的元素作为起点开始搜。
/** | |
* @param {character[][]} board | |
* @param {string} word | |
* @return {boolean} | |
*/ | |
var exist = function(board, word) { | |
function dfs(i, j, idx) { | |
if(idx == word.length) return true // 找到单词了 | |
if(i < 0 || i >= board.length || j < 0 || j >= board[0].length | |
|| board[i][j] == '#' || board[i][j] != word[idx]) | |
return false // 越界或者不匹配 | |
board[i][j] = '#' // 置为 #,避免重复访问 | |
let flag = false | |
if(dfs(i+1, j, idx+1) || dfs(i-1, j, idx+1) | |
|| dfs(i, j+1, idx+1) || dfs(i, j-1, idx+1)) // 四个方向试探 | |
flag = true | |
board[i][j] = word[idx] // 恢复 | |
return flag | |
} | |
for(let i = 0; i < board.length; ++i) { | |
for(let j = 0; j < board[0].length; ++j) { | |
if(board[i][j] === word[0]) | |
if(dfs(i, j, 0)) return true | |
} | |
} | |
return false | |
}; |
# 剑指 Offer 13. 机器人的运动范围
地上有一个 m 行 n 列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于 k 的格子。例如,当 k 为 18 时,机器人能够进入方格 [35, 37] ,因为 3+5+3+7=18。但它不能进入方格 [35, 38],因为 3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入: m = 2, n = 3, k = 1
输出: 3
示例 2:
输入: m = 3, n = 1, k = 0
输出: 1
提示:
1 <= n,m <= 1000 <= k <= 20
# 思路
广搜,注意搜索方向可以向右和向下就行了
/** | |
* @param {number} m | |
* @param {number} n | |
* @param {number} k | |
* @return {number} | |
*/ | |
var movingCount = function(m, n, k) { | |
function count(x) { | |
if(x == 0) return 0 | |
let sum = 0 | |
while(x) { | |
sum += x%10 | |
x = Math.floor(x/10) | |
} | |
return sum | |
} | |
let dx = [1, 0] | |
let dy = [0, 1] // 下 右 | |
let canVis = new Array(m).fill(0).map(() => new Array(n).fill(false)) | |
let vis = new Array(m).fill(0).map(() => new Array(n).fill(false)) | |
for(let i = 0; i < m; ++i) | |
for(let j = 0; j < n; ++j) | |
canVis[i][j] = (count(i) + count(j)) <= k | |
function judge(i, j) { | |
if(i < 0 || i >= m || j < 0 || j >= n || !canVis[i][j] || vis[i][j]) | |
return false | |
return true | |
} | |
let q = [] | |
let ans = 0 | |
vis[0][0] = true | |
q.push([0, 0]) | |
while(q.length) { | |
let [x, y] = q.shift() | |
++ans | |
for(let i = 0; i < 2; ++i) { | |
let nx = x + dx[i] | |
let ny = y + dy[i] | |
if(judge(nx, ny)) { | |
vis[nx][ny] = true | |
q.push([nx, ny]) | |
} | |
} | |
} | |
return ans | |
}; |
