上篇说到 RMQ 问题可以用 ST 表算法处理,但需要在线修改的时候,线段树是更好的选择。
如图,很明显线段树是个二叉搜索树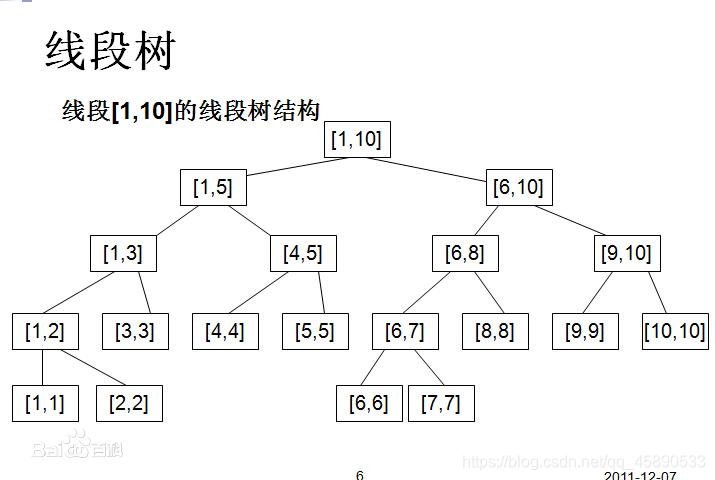
要注意的点如下:
- 线段树用数组存储,数组空间简单的就一般开到原数组的 4*n 倍(准确的说是将 n 向上扩充到 2 的幂次方然后乘 2,如 5->8->16)
- 线段树数组存储中,某个结点的编号为 n,则其左子结点编号为 2 n(表示成 n << 1), 右子节点编号为 2n+1 (表示为 n << 1 | 1)
- 规定根节点为 1
# 一、查询区间最值(点修改)
模板题:hihoCoder #1077 RMQ 问题再临 - 线段树
题目大意:给出一个数组 A,每次有查询或修改两种操作,此处是查询区间 l 到 r 上的最小值,或将编号为 p 的值改为 v。
用线段树维护最值,想要改成查询最大值,只需把所有 min 改成 max,然后把 inf 换成 0
# 1. 建树
void pushup(int rt) {// 更新节点信息 这里以求最小值为例 可改为最大值 | |
Tree[rt] = min(Tree[rt << 1], Tree[rt << 1|1]); | |
} | |
void Build(int l, int r, int rt) {//[l,r] 表示区间,rt 表示真实存储的编号 | |
if (l == r) {// 抵达叶结点 | |
Tree[rt] = A[l]; | |
return; | |
} | |
int mid = l+r>>1; | |
Build(l,mid,rt << 1);// 先建好左结点 | |
Build(mid+1,r,rt << 1 | 1);// 再建好右节点 | |
pushup(rt);// 用左右节点更新信息 | |
} |
# 2. 更新
调用时参数为根节点编号、修改位置 p、要修改成的值 v、修改影响的区间(即 1~n)。
void Update_point(int rt, int p, int val, int l, int r) { // 点修改 | |
if (l == r) { | |
Tree[rt] = val; | |
return; | |
} | |
int mid = (l+r) >> 1; | |
if (p <= mid)// 修改的位置如果是在左半区间,则更新左子树 | |
Update_point(rt<<1, p, val, l, mid); | |
else Update_point(rt<<1|1, p, val, mid+1, r);// 否则更新右子树 | |
pushup(rt);// 更新当前点~ | |
} |
# 3. 查询
难点所在,调用时参数分别为根结点、整个区间 (1 ~ n)、要查询的区间 (x ~ y)
ps: 要查询的区间是要一直传下去不会变的~当要查询的区间子区间为 l ~ r 时即可返回
int query(int rt, int l, int r,int x, int y) {// 从节点 rt 开始查询 L 到 R 的最小值 / 最大值 / 区间和 此处以最小值为例 | |
if (x <= l && r <= y) {// 当 l ~ r 为要查询的区间的子区间时可直接返回当前结点的值 | |
return Tree[rt]; | |
} | |
int mid = l+r >> 1; | |
int ans = inf;// 若求最大值,将此处改为 0 | |
if (x <= mid) // 若当前区间左端点小于等于 mid,则肯定要查询左半区间 | |
ans = min(query(rt<<1,l,mid,x,y), ans); | |
if (y > mid)// 若当前区间右端点大于 mid,则肯定要查询右半区间 | |
ans = min(query(rt<<1|1,mid+1,r,x,y), ans); | |
return ans; | |
} |
# 完整代码
#include <iostream> | |
#include <algorithm> | |
using namespace std; | |
// 定义 | |
const int maxn = 1000005; | |
const int inf = 0x3f3f3f; | |
int Tree[maxn<<2]; | |
int A[maxn]; | |
int n; | |
void pushup(int rt) {// 向上更新节点信息 这里以求最小值为例 可改为最大值 | |
Tree[rt] = min(Tree[rt << 1], Tree[rt << 1|1]); | |
} | |
void Build(int l, int r, int rt) {//[l,r] 表示区间,rt 表示真实存储的编号 | |
if (l == r) {// 抵达叶结点 | |
Tree[rt] = A[l]; | |
return; | |
} | |
int mid = l+r>>1; | |
Build(l,mid,rt << 1);// 先建好左结点 | |
Build(mid+1,r,rt << 1 | 1);// 再建好右节点 | |
pushup(rt);// 用左右节点更新信息 | |
} | |
void Update_point(int rt, int p, int val, int l, int r) { // 点修改 | |
if (l == r) { | |
Tree[rt] = val; | |
return; | |
} | |
int mid = (l+r) >> 1; | |
if (p <= mid)// 修改的位置如果是在左半区间,则更新左子树 | |
Update_point(rt<<1, p, val, l, mid); | |
else Update_point(rt<<1|1, p, val, mid+1, r);// 否则更新右子树 | |
pushup(rt);// 更新当前点~ | |
} | |
int query(int rt, int l, int r,int x, int y) {// 从节点 rt 开始查询 L 到 R 的最小值 / 最大值 / 区间和 此处以最小值为例 | |
if (x <= l && r <= y) {// 当 l ~ r 为要查询的区间的子区间时可直接返回当前结点的值 | |
return Tree[rt]; | |
} | |
int mid = l+r >> 1; | |
int ans = inf;// 若求最大值,将此处改为 0 | |
if (x <= mid) // 若当前区间左端点小于等于 mid,则肯定要查询左半区间 | |
ans = min(query(rt<<1,l,mid,x,y), ans); | |
if (y > mid)// 若当前区间右端点大于 mid,则肯定要查询右半区间 | |
ans = min(query(rt<<1|1,mid+1,r,x,y), ans); | |
return ans; | |
} | |
int main(){ | |
ios::sync_with_stdio(false); | |
cin >> n; | |
for(int i = 1; i <= n; i++) { | |
cin >> A[i]; | |
} | |
Build(1,n,1); | |
int T; | |
cin >> T; | |
while(T--) { | |
int a, b, c; | |
cin >> a >> b >> c; | |
if (a == 1) { | |
Update_point(1,b,c,1,n); | |
} else { | |
int ans = query(1,1,n,b,c); | |
cout << ans << endl; | |
} | |
} | |
return 0; | |
} |
# 二、区间修改(和、差、积、商等)
# 1. 区间加操作
洛谷 P3372 【模板】线段树 1
大意为:已知一个数列,你需要进行下面两种操作:
1. 将某区间每一个数加上 kk。
2. 求出某区间每一个数的和。
大神题解大神都写这么详细了我还写这个干嘛啊算了算了自己敲一遍留着看也不错嘛
我们可以用线段树来维护区间和,以及修改的话是进行修改区间修改~这就需要一个标记数组标记,其实点修改就是区间修改的一个子问题
# pushdown 操作
向下更新,因为懒标记 add 记录了对其子结点的影响,所以需要一个向下传递影响的函数
inline void f(int rt, int l, int r, ll k) {// 给当前结点加上 k 的影响,并更新其懒标记 | |
Tree[rt] += k * (r-l+1);// 区间和 这里维护的是区间和,区间内每个数都加上 k | |
add[rt] += k; | |
} | |
void pushdown(int rt, int l, int r) { | |
int mid = l+r >>1; | |
f(rt<<1, l, mid, add[rt]);// 更新左儿子的懒标记及其维护的值 (区间和) | |
f(rt<<1|1, mid+1, r, add[rt]);// 更新右儿子的懒标记及其维护的值 (区间和) | |
add[rt] = 0;// 当前懒标记置为 0 | |
} |
# 更新区间
void Update_section(int rt, int val, int l, int r, int rl, int rr) { // 区间修改 | |
if (rl <= l && r <= rr) {//~ 当前区间为要修改的区间的子区间时直接更新其值和懒标记~ | |
f(rt, l, r, val); | |
return; | |
} | |
pushdown(rt, l, r);// 下一次递归前,先将当前结点的影响向下传递,然后更新当前结点 | |
int mid = (l+r) >> 1; | |
if (rl <= mid)// 修改的区间如果能影响到左半区间,则更新左子树 | |
Update_section(rt<<1, val, l, mid, rl, rr); | |
if (rr > mid) | |
Update_section(rt<<1|1, val, mid+1, r, rl, rr);// 否则更新右子树 | |
pushup(rt);//~ 向上更新~ | |
} |
# 完整代码
#include <iostream> | |
#include <algorithm> | |
using namespace std; | |
// 定义 | |
typedef long long ll; | |
const int maxn = 1000005; | |
const int inf = 0x3f3f3f; | |
ll add[maxn<<2];// 懒标记 即对其所有子结点的影响 不包括其自身 | |
ll Tree[maxn<<2]; | |
ll A[maxn]; | |
int n, T; | |
inline void pushup(int rt) {// 向上更新节点信息 即用左孩子和右孩子的值来更新当前结点 | |
Tree[rt] = Tree[rt << 1]+Tree[rt << 1|1]; | |
} | |
inline void f(int rt, int l, int r, ll k) {// 给当前结点加上 k 的影响,并更新其懒标记 | |
Tree[rt] += k * (r-l+1);// 区间和 这里维护的是区间和,区间内每个数都加上 k | |
add[rt] += k; | |
} | |
void pushdown(int rt, int l, int r) { | |
int mid = l+r >>1; | |
f(rt<<1, l, mid, add[rt]);// 更新左儿子的懒标记及其维护的值 (区间和) | |
f(rt<<1|1, mid+1, r, add[rt]);// 更新右儿子的懒标记及其维护的值 (区间和) | |
add[rt] = 0;// 当前懒标记置为 0 | |
} | |
void Build(int l, int r, int rt) {//[l,r] 表示区间,rt 表示真实存储的编号 | |
add[rt] = 0; | |
if (l == r) {// 抵达叶结点 | |
Tree[rt] = A[l]; | |
return; | |
} | |
int mid = l+r>>1; | |
Build(l,mid,rt << 1);// 先建好左结点 | |
Build(mid+1,r,rt << 1 | 1);// 再建好右节点 | |
pushup(rt);// 用左右节点更新信息 | |
} | |
void Update_section(int rt, int val, int l, int r, int rl, int rr) { // 区间修改 | |
if (rl <= l && r <= rr) {//~ 当前区间为要修改的区间的子区间时直接更新其值和懒标记~ | |
f(rt, l, r, val); | |
return; | |
} | |
pushdown(rt, l, r);// 下一次递归前,先将当前结点的影响向下传递,然后更新当前结点 | |
int mid = (l+r) >> 1; | |
if (rl <= mid)// 修改的区间如果能影响到左半区间,则更新左子树 | |
Update_section(rt<<1, val, l, mid, rl, rr); | |
if (rr > mid) | |
Update_section(rt<<1|1, val, mid+1, r, rl, rr);// 否则更新右子树 | |
pushup(rt);//~ 向上更新~ | |
} | |
ll query(int rt, int l, int r,int x, int y) {// 从节点 rt 开始查询 l 到 r 的中 x~y 的区间和 此处以最小值为例 | |
if (x <= l && r <= y) {// 当 l ~ r 为要查询的区间的子区间时可直接返回当前结点的值 | |
return Tree[rt]; | |
} | |
int mid = l+r >> 1; | |
ll ans = 0; | |
pushdown(rt, l, r); | |
if (x <= mid) // 若当前区间左端点小于等于 mid,则肯定要查询左半区间 | |
ans += query(rt<<1,l,mid,x,y); | |
if (y > mid)// 若当前区间右端点大于 mid,则肯定要查询右半区间 | |
ans += query(rt<<1|1,mid+1,r,x,y); | |
return ans; | |
} | |
int main(){ | |
ios::sync_with_stdio(false); | |
cin >> n >> T; | |
for(int i = 1; i <= n; i++) { | |
cin >> A[i]; | |
} | |
Build(1,n,1); | |
while(T--) { | |
int a, l, r; | |
cin >> a; | |
if (a == 1) { | |
int k; | |
cin >> l >> r >> k; | |
Update_section(1, k, 1, n, l, r); | |
} else { | |
cin >> l >> r; | |
ll ans = query(1, 1, n, l, r); | |
cout << ans << endl; | |
} | |
} | |
return 0; | |
} |
# 2. 区间加、乘操作(较完整)
洛谷 P3373【模板】线段树 2
大神题解
这题就是在上一题的基础上变成可将某区间每个数乘 / 加上一个数,则需要两个懒标记数组 add、mul,而在更新懒标记操作中也要注意若要更新 add 标记则只更新 add, 若要更新 mul 则更新 mul 的同时也必须更新 add(add 乘上 k)
先乘后加!!
先乘后加!!!
先乘后加!!!
重要的事情说三遍
# pushdown 操作的变动
主要是 f 函数的变动
注意到 f 函数的功能是给当前结点 rt 的值加上上一个结点 ft 的所有影响(懒标记带来的),并更新当前结点 ft 的懒标记
inline void f(int rt, int l, int r, int ft) {// 给当前结点 rt 加上上一个结点 ft 的所有影响,更新其懒标记 | |
// 先乘后加!!更新其值 | |
Tree[rt] = (Tree[rt] * mul[ft]) % p; | |
Tree[rt] = (Tree[rt] + add[ft] * (r-l+1)) % p; | |
// 更新懒标记,mul 直接更新 (* 父结点的 mul) | |
mul[rt] = (mul[rt] * mul[ft]) % p; | |
//add 应先 * 父结点的 mul 标记,然后再 + 父节点的 add 标记!!! | |
add[rt] = (add[rt] * mul[ft]) % p; | |
add[rt] = (add[rt] + add[ft]) % p; | |
} | |
void pushdown(int rt, int l, int r) { | |
int mid = l+r >>1; | |
f(rt<<1, l, mid, rt);// 更新左儿子的懒标记及其维护的值 | |
f(rt<<1|1, mid+1, r, rt);// 更新右儿子的懒标记及其维护的值 | |
add[rt] = 0; | |
mul[rt] = 1;// 当前懒标记 | |
} |
# 更新操作变动(分两种更新)
加更新~
void Update_section_add(int rt,int val, int l, int r, int rl, int rr) { // 区间修改 +val | |
if (rl <= l && r <= rr) {//~ 当前区间为要修改的区间的子区间时直接更新其值和懒标记~ | |
Tree[rt] = (Tree[rt] + val * (r-l+1)) % p;// 给当前结点加上 val 的 + 影响,并更新其懒标记 | |
add[rt] = (add[rt] + val) % p; | |
return; | |
} | |
pushdown(rt, l, r);// 下一次递归前,先将影响向下传递 | |
int mid = (l+r) >> 1; | |
if (rl <= mid)// 修改的区间如果能影响到左半区间,则更新左子树 | |
Update_section_add(rt<<1, val, l, mid, rl, rr); | |
if (rr > mid) | |
Update_section_add(rt<<1|1, val, mid+1, r, rl, rr);// 否则更新右子树 | |
pushup(rt);// 开始回溯~向上更新~ | |
} |
乘更新~乘会影响到加的懒标记!
void Update_section_mul(int rt,int val, int l, int r, int rl, int rr) { // 区间修改 *val | |
if (rl <= l && r <= rr) {//~ 当前区间为要修改的区间的子区间时直接更新其值和懒标记~ | |
Tree[rt] = (Tree[rt] * val) % p; | |
mul[rt] = (mul[rt] * val) % p; | |
add[rt] = (add[rt] * val) % p;//very 重要!! | |
return; | |
} | |
pushdown(rt, l, r);// 下一次递归前,先将影响向下传递 | |
int mid = (l+r) >> 1; | |
if (rl <= mid)// 修改的区间如果能影响到左半区间,则更新左子树 | |
Update_section_mul(rt<<1, val, l, mid, rl, rr); | |
if (rr > mid) | |
Update_section_mul(rt<<1|1, val, mid+1, r, rl, rr);// 否则更新右子树 | |
pushup(rt);// 开始回溯~向上更新~ | |
} |
# 完整代码
#include <iostream> | |
#include <algorithm> | |
using namespace std; | |
// 定义 | |
typedef long long ll; | |
const int maxn = 1000005; | |
ll add[maxn<<2];// 懒标记 1 即对其所有子结点的影响 不包括其自身 | |
ll mul[maxn<<2];// 懒标记 2 | |
ll Tree[maxn<<2]; | |
ll A[maxn]; | |
int n, T; | |
ll p; | |
inline void pushup(int rt) {// 向上更新节点信息 即用左孩子和右孩子的值来更新当前结点 | |
Tree[rt] = Tree[rt << 1]+Tree[rt << 1|1]; | |
} | |
inline void f(int rt, int l, int r, int ft) {// 给当前结点 rt 加上上一个结点 ft 的 k 的所有影响,更新其懒标记 | |
// 先乘后加!! | |
Tree[rt] = (Tree[rt] * mul[ft]) % p; | |
Tree[rt] = (Tree[rt] + add[ft] * (r-l+1)) % p; | |
//mul 直接更新 | |
mul[rt] = (mul[rt] * mul[ft]) % p; | |
// 加的懒标记应先 * 父结点的 mul 标记,然后再 + 父节点的 add 标记!!! | |
add[rt] = (add[rt] * mul[ft]) % p; | |
add[rt] = (add[rt] + add[ft]) % p; | |
} | |
void pushdown(int rt, int l, int r) { | |
int mid = l+r >>1; | |
f(rt<<1, l, mid, rt);// 更新左儿子的懒标记及其维护的值 | |
f(rt<<1|1, mid+1, r, rt);// 更新右儿子的懒标记及其维护的值 | |
add[rt] = 0; | |
mul[rt] = 1;// 当前懒标记 | |
} | |
void Build(int l, int r, int rt) {//[l,r] 表示区间,rt 表示真实存储的编号 | |
add[rt] = 0; | |
mul[rt] = 1; | |
if (l == r) {// 抵达叶结点 | |
Tree[rt] = A[l]; | |
return; | |
} | |
int mid = l+r>>1; | |
Build(l,mid,rt << 1);// 先建好左结点 | |
Build(mid+1,r,rt << 1 | 1);// 再建好右节点 | |
pushup(rt);// 用左右节点更新信息 | |
} | |
void Update_section_add(int rt,int val, int l, int r, int rl, int rr) { // 区间修改 +val | |
if (rl <= l && r <= rr) {//~ 当前区间为要修改的区间的子区间时直接更新其值和懒标记~ | |
Tree[rt] = (Tree[rt] + val * (r-l+1)) % p;// 给当前结点加上 val 的 + 影响,并更新其懒标记 | |
add[rt] = (add[rt] + val) % p; | |
return; | |
} | |
pushdown(rt, l, r);// 下一次递归前,先将影响向下传递 | |
int mid = (l+r) >> 1; | |
if (rl <= mid)// 修改的区间如果能影响到左半区间,则更新左子树 | |
Update_section_add(rt<<1, val, l, mid, rl, rr); | |
if (rr > mid) | |
Update_section_add(rt<<1|1, val, mid+1, r, rl, rr);// 否则更新右子树 | |
pushup(rt);// 开始回溯~向上更新~ | |
} | |
void Update_section_mul(int rt,int val, int l, int r, int rl, int rr) { // 区间修改 *val | |
if (rl <= l && r <= rr) {//~ 当前区间为要修改的区间的子区间时直接更新其值和懒标记~ | |
Tree[rt] = (Tree[rt] * val) % p; | |
mul[rt] = (mul[rt] * val) % p; | |
add[rt] = (add[rt] * val) % p;//very 重要!! | |
return; | |
} | |
pushdown(rt, l, r);// 下一次递归前,先将影响向下传递 | |
int mid = (l+r) >> 1; | |
if (rl <= mid)// 修改的区间如果能影响到左半区间,则更新左子树 | |
Update_section_mul(rt<<1, val, l, mid, rl, rr); | |
if (rr > mid) | |
Update_section_mul(rt<<1|1, val, mid+1, r, rl, rr);// 否则更新右子树 | |
pushup(rt);// 开始回溯~向上更新~ | |
} | |
ll query(int rt, int l, int r,int x, int y) {// 从节点 rt 开始查询 l 到 r 的中 x~y 的区间和 此处以最小值为例 | |
if (x <= l && r <= y) {// 当 l ~ r 为要查询的区间的子区间时可直接返回当前结点的值 | |
return Tree[rt]; | |
} | |
int mid = l+r >> 1; | |
ll ans = 0; | |
pushdown(rt, l, r); | |
if (x <= mid) // 若当前区间左端点小于等于 mid,则肯定要查询左半区间 | |
ans = (ans + query(rt<<1,l,mid,x,y)) % p; | |
if (y > mid)// 若当前区间右端点大于 mid,则肯定要查询右半区间 | |
ans = (ans + query(rt<<1|1,mid+1,r,x,y)) % p; | |
return ans; | |
} | |
int main(){ | |
ios::sync_with_stdio(false); | |
cin >> n >> T >> p; | |
for(int i = 1; i <= n; i++) { | |
cin >> A[i]; | |
} | |
Build(1,n,1); | |
while(T--) { | |
int a, l, r; | |
cin >> a; | |
if (a == 1) { | |
int k; | |
cin >> l >> r >> k; | |
Update_section_mul(1, k, 1, n, l, r); | |
} else if(a == 2) { | |
int k; | |
cin >> l >> r >> k; | |
Update_section_add(1, k, 1, n, l, r); | |
} else { | |
cin >> l >> r; | |
ll ans = query(1, 1, n, l, r); | |
cout << ans << endl; | |
} | |
} | |
return 0; | |
} |
然后~恭喜 ac ~ 耶~!