# 前言
本次考试是线上双机位考试,为此又双叒叕买了个手机支架 - -
92 分,第 3 题和第 4 题始终优化不过,可能也是思路出了问题
# 题解
# 7-1 好数 (15 分)
好数是指由一对正整数 a<b 按照 a2+ab+b2 这个规则生成的数,a 和 b 就称为这个好数的源头。例如 91 就是一个好数,因为 5 2+5×6+6 2 = 91,于是数对(5,6)就是 91 的源头。而对于一个好数,其源头并不一定唯一,例如(1,9)就是 91 的另一个源头。
本题就要求你编写程序,判断一个给定的数字是否好,并且输出好数的所有源头。
输入格式
输入在第一行给出一个不超过 100 的正整数 N,随后 N 行,每行给出一个不超过 104 的正整数。
输出格式
对于每一个输入的数字,如果其是好数,则首先在一行中输出 Yes,然后每行输出它的一个源头,格式为 a b,按 a 的递增顺序输出;否则在一行中输出 No 和比该数大的最小的好数,其间以空格分隔,然后每行输出这个好数的一个源头,格式同上。
输入样例
3 | |
1 | |
91 | |
50 |
输出样例
No 7 | |
1 2 | |
Yes | |
1 9 | |
5 6 | |
No 52 | |
2 6 |
# 思路
我的思路是暴力即可,用 bool 数组 a 存某个数是否为好数,用 map 存每个好数对应的所有源头,然后遍历每对源头,将该对源头对应的好数标记为 true 并放入该好数对应的源头数组中,之后只要用 a 判断给出的 n 是不是好数,不是的话往后找即可。代码如下太暴力了呜呜呜不过能满分就行懒得优化了欸好像题解也很暴力那没事了
# 代码
#include <iostream> | |
#include <map> | |
#include <vector> | |
#include <utility> | |
using namespace std; | |
const int maxn = 100005; | |
int N; | |
bool a[maxn]; | |
map<int, vector<pair<int, int> > > m; | |
void Print(int h) { | |
vector<pair<int, int> > v = m[h]; | |
for(auto i: v) { | |
cout << i.first << ' ' << i.second << endl; | |
} | |
} | |
int main() { | |
cin >> N; | |
for(int i = 1; i < 105; ++i) { | |
for(int j = i+1; j < 106; ++j) { | |
int x = i*i+i*j+j*j; | |
// cout << x << endl; | |
m[x].push_back(make_pair(i, j)); | |
a[x] = true; | |
} | |
} | |
int k; | |
while(N--) { | |
cin >> k; | |
if(!a[k]) { | |
while(!a[k]) ++k; | |
cout << "No " << k << endl; | |
} else cout << "Yes" << endl; | |
Print(k); | |
} | |
return 0; | |
} |
# 7-2 数以类聚 (20 分)
我们把所有各位数字的乘积相同的数归为一类。例如 1362 和 2332 就是同一类,因为 1×3×6×2=2×3×3×2。给定 N 个正整数,请你判断它们可以被归成多少不同的类?
输入格式
输入在第一行给出一个正整数 N(≤105),第二行给出 N 个不超过 107
的正整数,数字间以空格分隔。
输出格式
在一行中输出 N 个给定的整数可以归类的数量、以及规模最大的类中最小的乘积。数字间以一个空格分隔。
输入样例
10 | |
1234 98 329 9552 47621 8862 5539 2333 5365 463 |
输出样例
7 54 |
# 思路
暴力
一个 tran 函数返回数 x 各位数字的乘积(如果有 0 的话直接返回 0)
然后输入的时候就可以开始记录,一个 map 表示每个类的规模,m [i] 表示乘积为 i 的数有多少个
# 代码
#include <iostream> | |
#include <sstream> | |
#include <map> | |
#include <vector> | |
#include <set> | |
#include <algorithm> | |
using namespace std; | |
typedef long long ll; | |
const ll maxn = 100005; | |
ll N, x; | |
map<ll, ll> m;// 每个类的规模 | |
set<ll> s;// 类的个数 | |
ll tran(ll x) { | |
string str; | |
stringstream ss; | |
ss << x; | |
ss >> str; | |
if(str.find('0') != string::npos) return 0; | |
int len = str.length(); | |
ll ans = 1; | |
for(int i = 0; i < len; ++i) { | |
ll c = str[i]-'0'; | |
ans *= c; | |
} | |
return ans; | |
} | |
int main() { | |
cin >> N; | |
for(int i = 0; i < N; ++i) { | |
cin >> x; | |
ll t = tran(x); | |
++m[t]; | |
s.insert(t); | |
} | |
ll maxi = -1; | |
ll ans = maxn; | |
for(auto i: s) { | |
if(m[i] >= maxi) | |
maxi = m[i]; | |
} | |
for(auto i: s) { | |
if(m[i] == maxi && i < ans) ans = i; | |
} | |
cout << s.size() << ' ' << ans << endl;; | |
return 0; | |
} |
# 7-3 自定义判题程序 (20 分)
在每次允许插入、删除、修改一个字符的前提下,用最少的动作把一个字符串变成另一个字符串,是一道著名的可以用动态规划解决的问题。但判题的麻烦之处在于,虽然最小代价是唯一的,但变换方法却是不唯一的。例如把 PAT 变成 PTA 最少需要 2 步,可以保持第 1 个字母不变,修改后面 2 个字母,也可以保持第 1、2 个字母不变,在 A 前面插入 T,后面删除 T。由于拼题 A 系统的默认判题程序只能通过比对输出文件来判断对错,对这种正确答案输出不唯一的题目就不能处理了,需要出题者额外编写一个自定义判题程序来解决问题。
本题就请你编写这个自定义判题程序,读入两个字符串和用户程序产生的输出结果,判断他们的程序输出是否正确。
输入格式
输入首先在前两行分别给出两个不超过 1000 个字符、以回车结束的非空字符串,第 1 行对应初始字符串,第 2 行对应目标字符串。
随后一行给出一个正整数 N(≤100),为需要判断的提交数。
接下来是 N 个提交的输出结果,每个结果占 2 行:第 1 行给出一个整数 K(不超出 32 位 int 的范围),为用户输出的动作数;第 2 行顺次描述对初始字符串的每个字符所做的操作:
- 如果这个字符不变,则在对应位置输出 0
- 如果这个字符被删除,则在对应位置输出 1
- 如果这个字符被改变,则在对应位置输出 2
- 如果这个字符前面或者后面插入了一个字符,则在插入的位置输出 3
注意我们要求用户提交的行首尾和数字间均无空格,所以如果有多余空格应判为错误。
题目保证这个操作序列不为空。
输出格式
对每个正确的提交,在一行中输出 AC;否则输出 WA。
注意:这里并不要求你会用动态规划求出最优解。所以对 “正确提交” 的判断,并不以动态规划求出的最优解为根据! 对于用户输出的 K,如果其操作序列的确给出了 K 步操作并可以完成字符串的变换,则称为一个 “可行解”。所谓 “正确提交”,是指所有提交的可行解中的最优解。
输入样例
This is a test. | |
Tom is a cat. | |
6 | |
8 | |
02330001100022100 | |
8 | |
11113330000001113300 | |
6 | |
022100000012200 | |
5 | |
033310000000200 | |
6 | |
0 2 2 1 000000 1 2 2 00 | |
6 | |
012200000022100 |
输出样例
WA | |
WA | |
AC | |
WA | |
WA | |
AC |
# 思路
最后 10 分钟愣是从 12 改到了 16 分,但还是有哪里不对劲,估计是结束的时候出的问题。
题意是给出两字符串和一系列操作,对每一个操作判断是否合法并且能否使初始字符串变为目标字符串,并且是否为最优解(所有提交的可行解中的最优解)
读入 s1、s2,然后开始读入操作,操作数 K 和操作字符串 t,先判断操作是否合法,即是否出现空格以及 012 之和是否等于操作数 K,然后在 judge 函数里判断每个步骤是否可行,手动模拟不变、删除、修改和插入。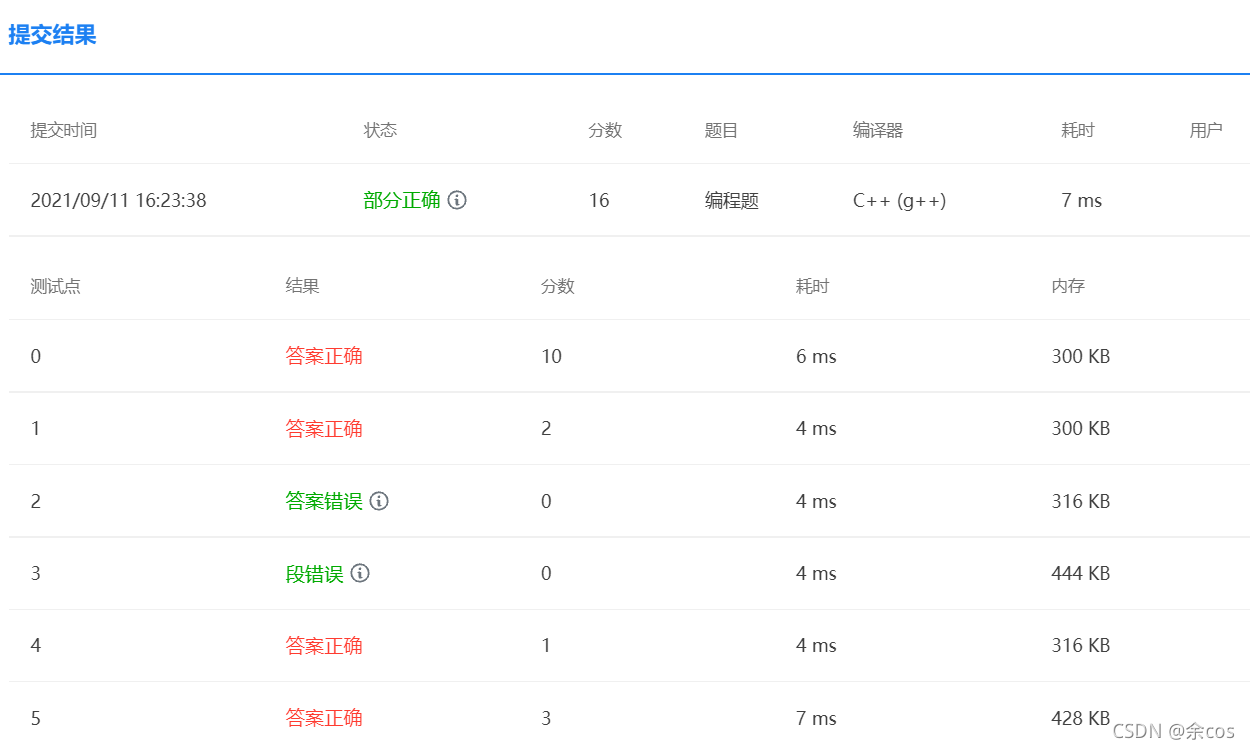
# 代码
#include <iostream> | |
#include <string> | |
#include <vector> | |
using namespace std; | |
typedef long long ll; | |
const ll inf = INT32_MAX; | |
string s1, s2, t; | |
int N, minK; | |
ll K; | |
vector<string> v; | |
vector<bool> b; | |
vector<int> ck; | |
bool judge(string s) { | |
for(int i = 0; i < s.size(); ++i) if(s[i] == ' ') return false; | |
int cnt = 0;// 操作数 | |
string temp; | |
int k1 = 0; | |
int k2 = 0; //s1 下标 | |
int len = s.length(); | |
int len1 = s1.length(); | |
int len2 = s2.length(); | |
for(int i = 0; i < len; ++i) { | |
if(s[i] == '0') { // 不变 | |
temp += s2[k2++]; | |
++k1; | |
} else if(s[i] == '1') { // 删除 | |
++cnt, ++k1; | |
} else if(s[i] == '2'){ // 被改变 | |
temp += s2[k2++]; | |
++cnt, ++k1; | |
} else { // 插入 | |
++cnt; | |
if(s1[k1] != s2[k2]) { // 在前面插入 | |
temp += s2[k2++]; | |
} else { // 相同的话在后面插入,或者如果后面也相同的话前插 | |
temp += s2[k2++]; | |
temp += s2[k2++]; | |
++k1; | |
} | |
} | |
} | |
// cout << temp << endl; | |
if(temp == s2 && cnt == K) return true; | |
else return false; | |
} | |
int main() { | |
getline(cin, s1); | |
getline(cin, s2); | |
cin >> N; | |
minK = inf; | |
for(int i = 0; i < N; ++i) { | |
cin >> K; | |
ck.push_back(K); | |
cin.ignore(); | |
getline(cin, t); | |
v.push_back(t); | |
// cout << K << t << endl; | |
b.push_back(judge(t)); | |
if(b[i] && K < minK) minK = K; | |
} | |
// cout << minK << endl; | |
for(int i = 0; i < v.size(); ++i) { | |
if(b[i] && ck[i] == minK) cout << "AC" << endl; | |
else cout << "WA" << endl; | |
} | |
return 0; | |
} |
# 7-4 数组与链表 (20 分)
让我们来设计这样一种数组与链表结合的整数存储的结构 A:
这种结构首先初始化一个长度为 L0 的整型数组 A0,返回给用户使用。当用户访问第 i 个元素 A [i] 的时候,如果 0≤i<L0,则 A [i] 对应 A0 [i],系统就返回 h0 + i × sizeof (int) 作为要访问的地址,其中 h0 是数组 A0 的起始位置,sizeof (int) 是数组元素的大小,这里元素就是 int 型,占 4 个字节。
当用户访问越界时(即 i≥L0),系统将另外开辟一个长度为 L1 的数组 A 1。此时 A [i] 对应 A1 [j](这里 i 和 j 之间的映射关系留给你去推导)。如果 0≤j<L1 ,则返回 h1+j×sizeof (int) 作为要访问的地址,其中 h1 是数组 A1 的起始位置。
当 A1 [j] 继续越界时,系统就按照上述规则继续开辟另一个长度为 L2 的数组 A2 ,并以此类推。
本题就请你实现这个系统功能,为用户的任何一次访问返回对应元素的地址。
输入格式
输入第一行给出两个正整数 N(≤104)和 K(≤103),分别为最多允许开出的数组个数、以及用户访问的次数。
此后 N 行,每行给出两个正整数,分别是一个数组的初始地址(≤107)和长度(≤100),其间以空格分隔。题目保证这些数组占据的空间无重叠。
最后一行顺序给出 K 个用户访问的数组下标,为区间 [0,220] 内的整数。
输出格式
对每个用户访问,在一行中输出对应的地址。但如果用户的访问超出了 N 个数组的存储范围,则这个访问是非法的,要输出 Illegal Access ,并且对这个访问不采取任何处理。
最后一行请输出上述过程中一共创建了多少个数组。
输入样例
6 7 | |
2048 5 | |
128 6 | |
4016 10 | |
1024 7 | |
3072 12 | |
9332 10 | |
2 12 25 50 28 8 39 |
输出样例
2056 | |
4020 | |
1040 | |
Illegal Access | |
3072 | |
140 | |
3116 | |
5 |
# 思路
md 也是 16 分代码,让我康康错哪了
将链表以数组的形式给出,提供每个区间的首地址和可容纳元素的个数,int 型数据占 4 个字节,需判断是否能装入该数组以及时装入的地址。首先读入所有数据并求出可容纳的元素个数,然后依次读入 K 个用户访问的数组下标,判断是否越这个数组界,是的话加开数组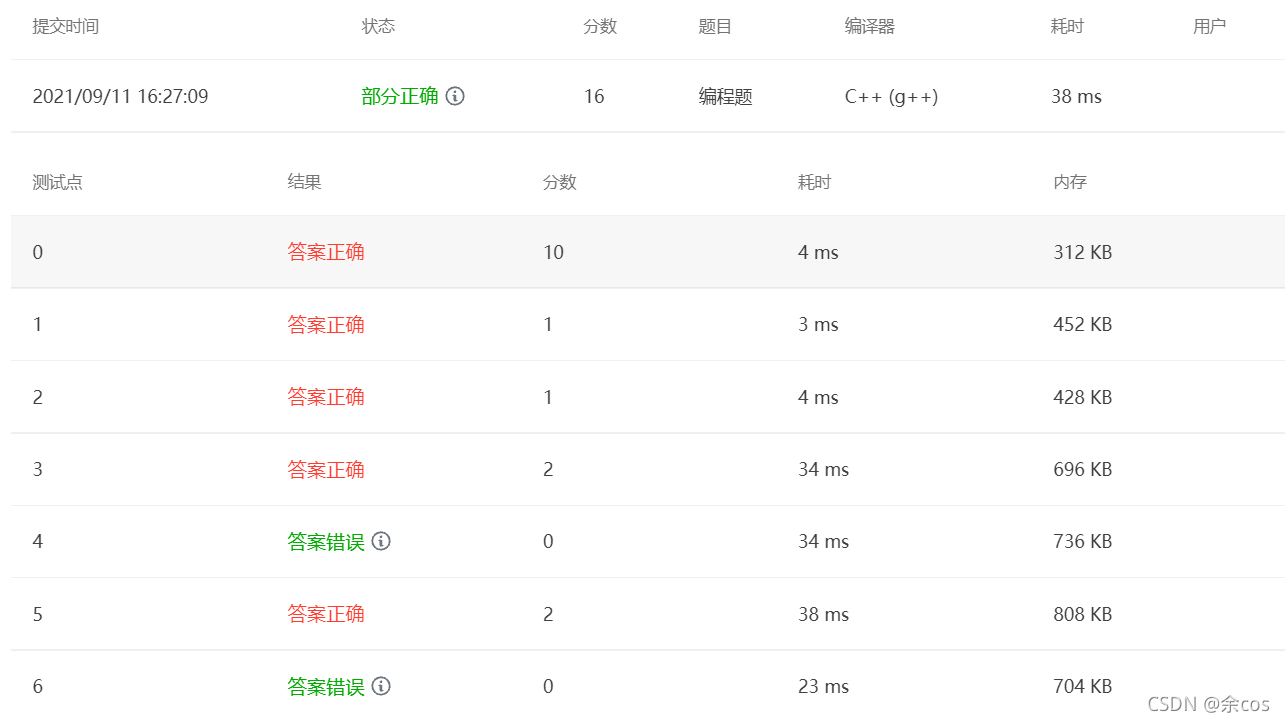
# 代码
#include <iostream> | |
#include <string> | |
#include <vector> | |
using namespace std; | |
typedef long long ll; | |
int N, K; | |
ll x, nowx, cnt; | |
struct Arr { | |
ll adr; | |
int len; | |
} a; | |
vector<Arr> v; | |
int main() { | |
cin >> N >> K; | |
for(int i = 0; i < N; ++i) { | |
cin >> a.adr >> a.len; | |
v.push_back(a); | |
} | |
int realans = 1; | |
for(int i = 0; i < K; ++i) { | |
int ans = 1; | |
bool flag = false; | |
cin >> x; | |
cnt = 0; | |
for(int j = 0; j < v.size(); ++j) { | |
if(flag) break; | |
if(x >= cnt+v[j].len) { // 越这个数组界了 加开数组 | |
cnt += v[j].len; | |
++ans; | |
continue; | |
} else { | |
// cout << cnt << ' '; | |
flag = true; | |
cout << v[j].adr+(x-cnt)*4 << endl; | |
} | |
} | |
if(!flag) cout << "Illegal Access" << endl; | |
else realans = ans; | |
} | |
cout << realans << endl; | |
return 0; | |
} | |
//2048+8 |
# 7-5 取帽子 (25 分)
拼题 er 们觉得戴帽子会令自己看上去很帅,所以他们不管到哪里都会戴着帽子。有一天他们去到一家餐厅,服务员把他们的帽子收集了堆起来保管。当大家要离开的时候,发现帽子被像上图那样摞起来了。于是你的任务就是帮他们排好队,使得每个人都能按顺序顺利取到自己的帽子。
已知每顶帽子的大小都不相同,并且帽子的尺寸跟帽子主人的体重有关 —— 越重的人戴的帽子就越大。
输入格式
输入第一行给出一个正整数 N (≤104),为拼题 er 的人数。随后一行给出 N 个不同的帽子尺寸,为不超过 105 的正整数,顺序是从帽子堆的底部向上给出。最后一行给出 N 个不同的体重,顺序对应编号从 1 到 N 的拼题 er。体重是不超过 106 的正整数。一行中的数字以空格分隔。
输出格式
在一行中按照取帽子的顺序输出帽子主人的编号。数字间以 1 个空格分隔,行首尾不得有多余空格。
输入样例
10 | |
12 19 13 11 15 18 17 14 16 20 | |
67 90 180 98 87 105 76 88 150 124 |
输出样例
3 4 8 6 10 2 1 5 9 7 |
# 思路
最简单的居然是 25 题 - -
给出 N 顶帽子大小(从底往上)和 N 个人的体重(编号 1-N),体重越大对应帽子编号,要求输出这 n 个人的排队顺序以便他们都能拿到自己的帽子
只需要两个数组 v1、v2 表示帽子大小、体重,两个 map 映射 m2、m3,m2 [i] 表示表示体重为 i 的人的编号,m3 [i] 表示按排好序后帽子大小 i 后对应的编号。
# 代码
#include <iostream> | |
#include <algorithm> | |
#include <vector> | |
#include <map> | |
using namespace std; | |
const int maxn = 10005; | |
int N, x; | |
int a[maxn]; | |
int b[maxn]; | |
vector<int> v1; | |
vector<int> v2; | |
map<int, int> m2; | |
map<int, int> m3; | |
int main() { | |
cin >> N; | |
for(int i = 0; i < N; ++i) { | |
cin >> a[i]; | |
v1.push_back(a[i]); | |
} | |
for(int i = 0; i < N; ++i) { | |
cin >> b[i]; | |
v2.push_back(b[i]); | |
m2[b[i]] = i; | |
} | |
sort(v1.begin(), v1.end()); | |
for(int i = 0; i < v1.size(); ++i) { | |
m3[v1[i]] = i; //20 对应 v1 排好序的下表 | |
} | |
sort(v2.begin(), v2.end()); | |
cout << m2[v2[m3[a[N-1]]]]+1; | |
for(int i = N-2; i >= 0; --i) { | |
cout << ' ' << m2[v2[m3[a[i]]]]+1; | |
} | |
cout << endl; | |
return 0; | |
} |