首页 题目记录

题目集总目录
学习指路博客 堆与哈夫曼树与并查集

# 05 - 树 7 堆中的路径 (25 分)

本题链接

将在 “小白专场” 中介绍 C 语言的实现方法，是建立最小堆的基本操作训练，一定要做

# 题目大意

给出最小堆的插入序列，和下标序列，每个下标 i 输出 Data [i] 到根结点路径上的值。

# 代码

#include <iostream>
using namespace std;
const int mindata = -10005;
const int maxsize = 10000;
typedef struct HeapStruct *MinHeap;
struct HeapStruct {
    int *Data;
    int Size;
};
MinHeap Create(int maxsize) {
    MinHeap H = new HeapStruct;
    H->Data = new int[maxsize];
    H->Size = 0;
    H->Data[0] = mindata;
    return H;
}
void Insert(int data, MinHeap H) {
    int i;
    i = ++H->Size;
    for(; H->Data[i>>1] > data; i >>= 1) {
        H->Data[i] = H->Data[i>>1];
    }
    H->Data[i] = data;
}
void PrintPath(int index, MinHeap H) {
    bool flag = false;
    while(index != 0) {
        if(flag) cout << " " << H->Data[index];
        else cout << H->Data[index];
        flag = true;
        index >>= 1;
    }
    cout << endl;
}
int main() {
    MinHeap H = Create(maxsize);
    int N, M, x;
    cin >> N >> M;
    for(int i = 0; i < N; ++i) {
        cin >> x;
        Insert(x, H);
    }
    for(int i = 0; i < M; ++i) {
        cin >> x;
        PrintPath(x, H);
    }
    return 0;
}

# 测试点

测试点如下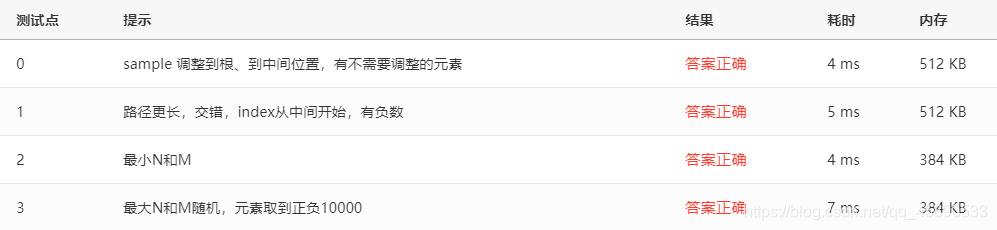
在这里插入图片描述

# 05 - 树 8 File Transfer (25 分)

本题链接

关于并查集，2005、2007 年浙江大学计算机学院免试研究生上机考试题即由此题改编而来。“小白专场” 中介绍了原始并查集算法的优化，听完课以后自己尝试一下

# 题目大意

每个样例中，C 为查询任意两个计算机是否联通，I 为连通这两个计算机，最后 S 结束后检查是否全部连通，如没有全部不连通则输出有多少个连通的。

# 思路

并查集 + 路径压缩

# 代码

#include <iostream>
using namespace std;
const int maxn = 10005;
int fa[maxn];
int N, x, y;
char ch;
inline void init() {
    for(int i = 1; i <= N; ++i) 
        fa[i] = i;
}
int find(int x) {// 查询 + 路径压缩 把沿途的每个节点的父节点都设为根节点
    return x == fa[x] ? x : (fa[x] = find(fa[x]));
}
void Merge(int x, int y) {
    fa[find(x)] = find(y);
}
int main() {
    scanf("%d", &N);
    init();
    getchar();
    scanf("%c", &ch);
    while(ch != 'S') {
        scanf("%d %d", &x, &y);
        getchar();
        if(ch == 'C') {
            if(find(x) == find(y)) cout << "yes" << endl;
            else cout << "no" << endl;
        } else if(ch == 'I') Merge(x, y);
        scanf("%c", &ch);
    }
    int ans = 0;
    for(int i = 1; i <= N; ++i) {
        if(fa[i] == i) ans++;
    }
    if(ans == 1) cout << "The network is connected." << endl;
    else cout << "There are " << ans << " components." << endl;
    return 0;
}

# 测试点

测试点如下
在这里插入图片描述

# 05 - 树 9 Huffman Codes (30 分)

本题链接

考察对 Huffman 编码的理解，程序可能略繁，量力而为。
题目大意： 给出若干字符及其频率，判断学生给的编码方式是否为最优编码

# 思路

看了陈越姥姥的讲解才知道，先根据给定的字符及其频率构建哈夫曼树，得到最优解的 WPL (编码长度)，再判断学生给的编码，在长度一致的情况下，判断是否为前缀码。这里我用优先队列代替小顶堆的一大串代码，求 wpl 时用的是另一种方法。在这里插入图片描述
在这里插入图片描述

# 代码

#include <iostream>
#include <map>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long ll;
#define div 1000000007
const int maxn = 70;
const int inf  = 0x3f3f3f;
int N,M,codelen;
struct Code {
 char ch;
 string s;
 int f;// 频率
}a[maxn];
typedef struct TreeNode* CodeTree;
struct TreeNode {
 int Weight;
 CodeTree Left, Right;
};
CodeTree head;
priority_queue<int,vector<int>, greater<int> > q; // 优先队列代替小顶堆
int WPL() {
 int wpl = 0;
 while(q.size() > 1) {
  int t1 = q.top();
  q.pop();
  int t2 = q.top();
  q.pop();
  wpl += (t1+t2);
  q.push(t1+t2); 
 }
 return wpl;
}
bool check() {// 检查是否是前缀码
 head = new TreeNode;
 head->Left = head->Right = NULL;
 head->Weight = -1;
 CodeTree p = head;
 for (int i = 0; i < N; ++i) {
  string code = a[i].s;
  int len = code.length();
  for (int i = 0; i < len; ++i) {
   if (code[i] == '1') {
    if (!p->Right) {
     p->Right = new TreeNode;
     p->Right->Left = p->Right->Right = NULL;
     p->Right->Weight = -1;
    }
    p = p->Right;
    // 中途有别的结点 有前缀码
   }
   else {
    if (!p->Left){
     p->Left = new TreeNode;
     p->Left->Right = p->Left->Left = NULL;
     p->Left->Weight = -1;
    }
    p = p->Left;
   }
   if (p->Weight != -1) return false;
  }
  p->Weight = 1;
  if (p->Left || p->Right) return false;
  p = head;
 }
 return true;
}
int main(){
    ios::sync_with_stdio(false);
    cin >> N;
    for(int i = 0; i < N; ++i) {
        cin >> a[i].ch >> a[i].f;
  q.push(a[i].f);
    }
 int codelen = WPL();
 cin >> M;
 while(M--) {
  int len = 0;
  for(int i = 0; i < N; ++i){
   cin >> a[i].ch >> a[i].s;
   len += a[i].f * a[i].s.length();
  }
  if(len == codelen && check()) cout << "Yes" << endl;
  else cout << "No" << endl;
 }
    return 0;
}

# 测试点

测试点如下
在这里插入图片描述