day12 题目：64. 最小路径和、300. 最长递增子序列、bytedance-004. 机器人跳跃问题

学习计划链接：冲刺春招 - 精选笔面试 66 题大通关

今日知识点：数组、动态规划、二分，难度为中等、中等、字节の简单

昨日题目链接：冲刺春招 - 精选笔面试 66 题大通关 day11

# 64. 最小路径和

给定一个包含非负整数的  m x n  网格  grid  ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明： 每次只能向下或者向右移动一步。

示例 1：

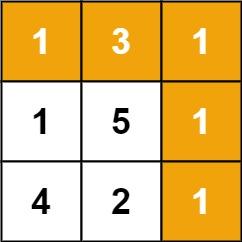
输入： grid = [[1,3,1],[1,5,1],[4,2,1]]
输出： 7
解释： 因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入： grid = [[1,2,3],[4,5,6]]
输出： 12

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

# 思路

一眼动态规划的题目

• dp [i][j] 表示到达 (i,j) 这个点的最小路径和
• 转移公式为 dp [i][j] = min (dp [i-1][j], dp [i][j-1]) + grid [i][j]
• 先初始化第一行第一列，由于 dp 过程中只涉及相邻的两个结点，故可以将 grid 原来的值直接覆盖。

# 代码

/**

 * @param {number[][]} grid

 * @return {number}

 */

 var minPathSum = function(grid) {

    let [m, n] = [grid.length, grid[0].length];

    for(let i = 1; i < m; ++i) 

        grid[i][0] = grid[i-1][0] + grid[i][0]; // 第一列

    for(let i = 1; i < n; ++i) 

        grid[0][i] = grid[0][i-1] + grid[0][i]; // 第一行

    for(let i = 1; i < m; ++i)

        for(let j = 1; j < n; ++j)

            grid[i][j] = Math.min(grid[i-1][j], grid[i][j-1]) + grid[i][j];    // 左侧和上侧中走过来较小的呢个

    return grid[m-1][n-1];

};

# 300. 最长递增子序列

给你一个整数数组  nums  ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如， [3,6,2,7]  是数组  [0,3,1,6,2,2,7]  的子序列。

示例 1：

输入： nums = [10,9,2,5,3,7,101,18]
输出： 4
解释： 最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入： nums = [0,1,0,3,2,3]
输出： 4

示例 3：

输入： nums = [7,7,7,7,7,7,7]
输出： 1

提示：

• 1 <= nums.length <= 2500
• -104 <= nums[i] <= 104

进阶：

• 你能将算法的时间复杂度降低到  O(n log(n))  吗？

# 思路

动态规划， dp[i] 表示 0~i 中最长递增子序列长度，每次在 0 到 i-1 中找可以与当前 i 构成递增序列的 j ，取其中最大的那个作为 dp[i]

# 代码

/**

 * @param {number[]} nums

 * @return {number}

 */

 var lengthOfLIS = function(nums) {

    let len = nums.length;

    let dp = new Array(len).fill(1);    //dp [i] 表示 0~i 中最长递增子序列长度

    let ans = 1;

    for(let i = 1; i < len; ++i) {

        for(let j = 0; j <= i-1; ++j) {

            if(nums[i] > nums[j])  // 大，可以与当前 i 构成递增序列

                dp[i] = Math.max(dp[i], dp[j]+1);

        }

        ans = Math.max(ans, dp[i]);

    }

    return ans;

};

# bytedance-004. 机器人跳跃问题

机器人正在玩一个古老的基于 DOS 的游戏。游戏中有 N+1 座建筑 —— 从 0 到 N 编号，从左到右排列。编号为 0 的建筑高度为 0 个单位，编号为 i 的建筑的高度为 H (i) 个单位。
起初， 机器人在编号为 0 的建筑处。每一步，它跳到下一个（右边）建筑。假设机器人在第 k 个建筑，且它现在的能量值是 E, 下一步它将跳到第个 k+1 建筑。它将会得到或者失去正比于与 H (k+1) 与 E 之差的能量。如果 H (k+1) > E 那么机器人就失去 H (k+1) - E 的能量值，否则它将得到 E - H (k+1) 的能量值。
游戏目标是到达第个 N 建筑，在这个过程中，能量值不能为负数个单位。现在的问题是机器人以多少能量值开始游戏，才可以保证成功完成游戏？

格式：

输入：
- 第一行输入，表示一共有 N 组数据.
- 第二个是 N 个空格分隔的整数，H1, H2, H3, ..., Hn 代表建筑物的高度
输出：
- 输出一个单独的数表示完成游戏所需的最少单位的初始能量

示例 1：
输入

5
3 4 3 2 4

输出

4

示例 2：

输入

3
4 4 4

输出

4

示例 3：

3
1 6 4

提示：

• 1 <= N <= 10^5
• 1 <= H(i) <= 10^5

# 思路

没什么思路，去看了一眼评论恍然大悟。这题核心是解一下方程，虽然题意忽悠我们说了一大堆，实际上是这样的：
设当前编号为 i ，高度为 h[i] ，能量为 e[i] ，则想到下一个点有 e[i+1] = e[i]+(e[i]-h[i+1]) 或者 e[i+1] = e[i]-(h[i+1]-e[i]) ，可以发现这两者其实都是等价 e[i+1] = 2*e[i]-h[i+1] 的，故当最后一个也就是 e[n-1] 为 0 时初始所需能量最少，即 2*e[i]-h[i+1] = 0 时，解得 e[i] = h[i+1]/2 （向上取整）那么从后往前遍历一遍即可。

# 代码

#include <iostream>

using namespace std;

const int maxn = 100005;

int n, h[maxn], E;

int main() {

    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);

    cin >> n;

    for(int i = 0; i < n; ++i) 

        cin >> h[i];

    for(int i = n-1; i >= 0; --i)

        E = (E+h[i]+1)/2;

    cout << E << endl;

    return 0;

}