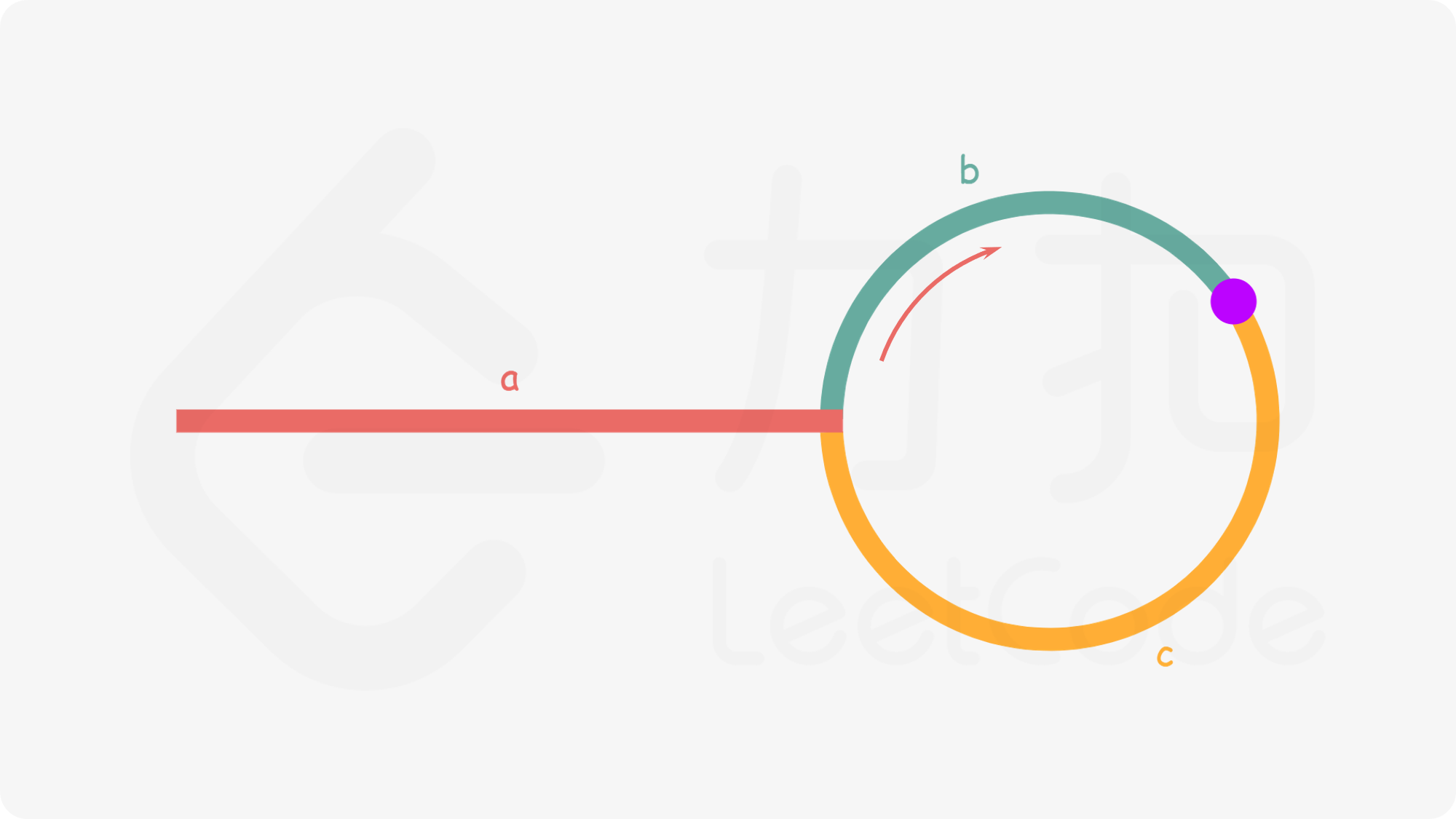day19 题目：160. 相交链表、143. 重排链表、142. 环形链表 II

今日知识点：链表、递归、双指针，难度为简单、中等、中等

学习计划链接：冲刺春招 - 精选笔面试 66 题大通关

昨日题目链接：冲刺春招 - 精选笔面试 66 题大通关 day18

# 160. 相交链表

给你两个单链表的头节点  headA  和  headB  ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回  null  。

图示两个链表在节点  c1  开始相交 ：

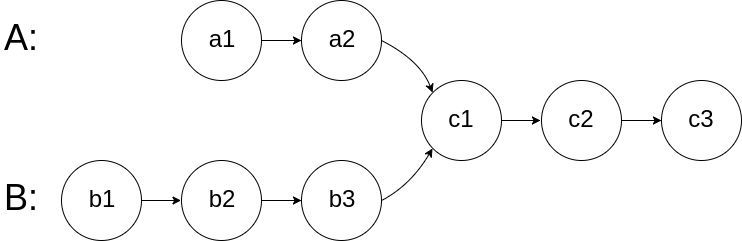
题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：

评测系统 的输入如下（你设计的程序 不适用 此输入）：

• intersectVal  - 相交的起始节点的值。如果不存在相交节点，这一值为  0
• listA  - 第一个链表
• listB  - 第二个链表
• skipA  - 在  listA  中（从头节点开始）跳到交叉节点的节点数
• skipB  - 在  listB  中（从头节点开始）跳到交叉节点的节点数

评测系统将根据这些输入创建链式数据结构，并将两个头节点  headA  和  headB  传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

示例 1：

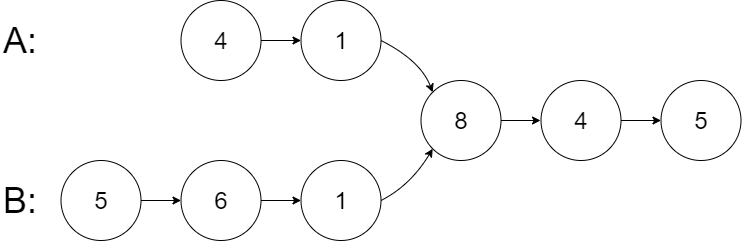
输入： intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出： Intersected at '8'
解释： 相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

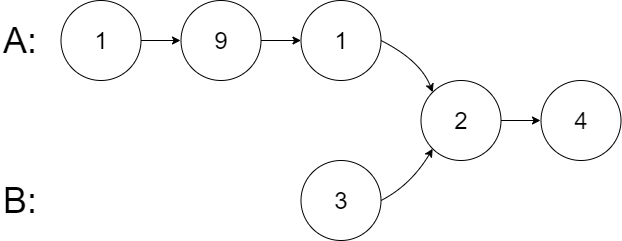
输入： intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出： Intersected at '2'
解释： 相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

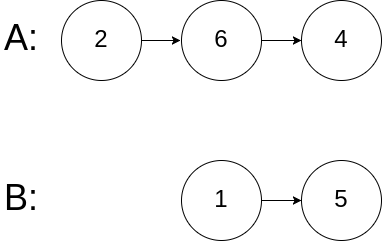
输入： intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出： null
解释： 从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

提示：

• listA  中节点数目为  m
• listB  中节点数目为  n
• 1 <= m, n <= 3 * 10^4
• 1 <= Node.val <= 10^5
• 0 <= skipA <= m
• 0 <= skipB <= n
• 如果  listA  和  listB  没有交点， intersectVal  为  0
• 如果  listA  和  listB  有交点， intersectVal == listA[skipA] == listB[skipB]

进阶： 你能否设计一个时间复杂度  O(m + n)  、仅用  O(1)  内存的解决方案？

# 思路

双指针，利用 prea 和 preb 作为 a 和 b 的前一个结点，当 prea === preb 时说明这当前节点上一个节点都是同一个结点

# 代码

/**

 * Definition for singly-linked list.

 * function ListNode(val) {

 *     this.val = val;

 *     this.next = null;

 * }

 */

/**

 * @param {ListNode} headA

 * @param {ListNode} headB

 * @return {ListNode}

 */

var getIntersectionNode = function(headA, headB) {

    if(!headA || !headB) return null

    let [prea, preb] = [headA, headB]

    while(prea !== preb) {

        prea = prea.next

        preb = preb.next

        if(prea === preb) return prea

        if(!prea) prea = headB

        if(!preb) preb = headA

    }

    return prea

};

# 143. 重排链表

给定一个单链表  L ** 的头节点  head  ，单链表  L  表示为：

L0 → L1 → … → Ln - 1 → Ln

请将其重新排列后变为：

L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …

不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

示例 1：

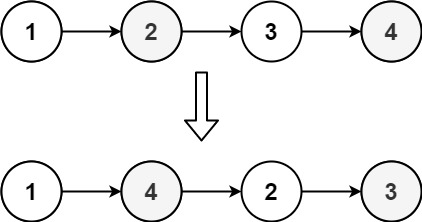
输入： head = [1,2,3,4]
输出： [1,4,2,3]

示例 2：

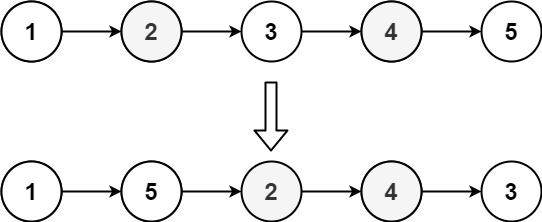
输入： head = [1,2,3,4,5]
输出： [1,5,2,4,3]

提示：

• 链表的长度范围为  [1, 5 * 10^4]
• 1 <= node.val <= 1000

# 思路

• 若没有结点或只有一两个结点，则无需操作。
• 每次将最后一个结点 nowv 接在头结点 head 后面
• 然后将倒数第二个结点 prev 置为最后一个节点
• 再对递归的原本的第三个结点 nowv.next 以及之后的链表进行该操作

# 代码

/**

 * @param {ListNode} head

 * @return {void} Do not return anything, modify head in-place instead.

 */

var reorderList = function(head) {

    if(!head || !head.next) return;

    let [prev, nowv] = [null, head];

    while(nowv.next) {

        prev = nowv

        nowv = nowv.next

    }

    if(!prev || prev === head)  return

    prev.next = null

    nowv.next = head.next

    head.next = nowv

    reorderList(nowv.next)

};

# 142. 环形链表 II

给定一个链表的头节点   head  ，返回链表开始入环的第一个节点。 如果链表无环，则返回  null 。

如果链表中有某个节点，可以通过连续跟踪  next  指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数  pos  来表示链表尾连接到链表中的位置（索引从 0 开始）。如果  pos  是  -1 ，则在该链表中没有环。注意： pos  不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

输入： head = [3,2,0,-4], pos = 1
输出： 返回索引为 1 的链表节点
解释： 链表中有一个环，其尾部连接到第二个节点。

示例 2：

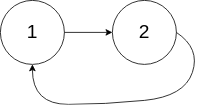
输入： head = [1,2], pos = 0
输出： 返回索引为 0 的链表节点
解释： 链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入： head = [1], pos = -1
输出： 返回 null
解释： 链表中没有环。

提示：

• 链表中节点的数目范围在范围  [0, 10^4]  内
• -10^5 <= Node.val <= 10^5
• pos  的值为  -1  或者链表中的一个有效索引

进阶： 你是否可以使用  O(1)  空间解决此题？

# 思路

环形链表在冲刺春招 - 精选笔面试 66 题大通关 day17 中有做过，主要思想是快慢指针，快指针一次走两步，慢指针一次走一步，若有环则一定会遇上，否则没有环。

而这里需要返回入环处的结点，那么，当快指针 fast 等于慢指针 slow 时，设置一个新的指针 ptr 跟着 slow 一块走，最终 ptr 和 slow 就会在入环结点相遇。
推导如下，直接看官方的吧：

如下图所示，设链表中环外部分的长度为 a 。 slow  指针进入环后，又走了  b  的距离与  fast  相遇。此时，假设 fast  指针已经走完了环的  n  圈，则 fast 走过的总距离为 a+n(b+c)+b 化简得 a+(n+1)b+nc 。

由于快指针每次都比慢指针多走一步，故 fast 走过的距离是 slow 的两倍，而 slow 走过的总距离为 a+b ，所以有 a+(n+1)b+nc = 2(a+b) ，解得 a = c+(n-1)(b+c)

• 也就是说，从相遇点到入环点的距离 c 加上 n-1 圈环长（b+c），恰好等于链表头部到入环点的距离 a
• 因此，当发现  slow 与 fast 相遇时，我们再额外使用一个指针  ptr 。起始， ptr 指向链表头部。随后， ptr 和  slow  每次向后移动一个位置。最终，它们会在入环点相遇。

# 代码

/**

 * @param {ListNode} head

 * @return {ListNode}

 */

var detectCycle = function(head) {

    let [slow, fast] = [head, head];

    while(fast && fast.next) {

        slow = slow.next

        fast = fast.next.next

        if(slow === fast) break

    }

    if(!fast || !fast.next) return null

    let p = head

    while(p !== slow) {

        p = p.next

        slow = slow.next

    }

    return p

};