day19 题目: 剑指 Offer 64. 求 1+2+…+n、剑指 Offer 68 - I. 二叉搜索树的最近公共祖先、剑指 Offer 68 - II. 二叉树的最近公共祖先
知识点:树、递归、dfs/bfs,难度为中等、简单、简单
学习计划链接:「剑指 Offer」 - 学习计划
| 题目 | 知识点 | 难度 |
|---|---|---|
| 剑指 Offer 64. 求 1+2+…+n | 位运算、递归、脑筋急转弯 | 中等 |
| 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先 | 树、深度优先搜索、二叉搜索树 | 简单 |
| 剑指 Offer 68 - II. 二叉树的最近公共祖先 | 树、深度优先搜索、二叉树 | 简单 |
# 剑指 Offer 64. 求 1+2+…+n
求 1+2+...+n ,要求不能使用乘除法、for、while、if、else、switch、case 等关键字及条件判断语句(A?B:C)。
示例 1:
输入: n = 3
输出: 6
示例 2:
输入: n = 9
输出: 45
限制:
1 <= n <= 10000
# 思路与代码
看这题的 tag:脑筋急转弯就能发现不对劲……
主要就是用短路运算符来代替条件判断
/** | |
* @param {number} n | |
* @return {number} | |
*/ | |
var sumNums = function(n) { | |
n && (n += sumNums(n-1)) | |
return n | |
}; |
# 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
给定一个二叉搜索树,找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
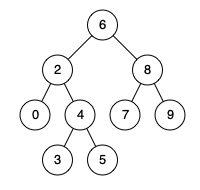
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
注意:本题与主站 235 题相同:https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree/
# 思路与代码
根据之前冲刺春招 - 精选笔面试 66 题大通关 17 的经验,思路一为先从一个节点往上走将沿途的 vis 置为 true,再从另一个结点往上走,遇到 vis 为 true 的就是最近共同祖先,返回。
/** | |
* @param {TreeNode} root | |
* @param {TreeNode} p | |
* @param {TreeNode} q | |
* @return {TreeNode} | |
*/ | |
var lowestCommonAncestor = function(root, p, q) { | |
if(!root) return null | |
let fa = new Map() | |
function dfs(rt, pre) { | |
if (rt === null) return | |
fa.set(rt, pre) | |
dfs(rt.left, rt) | |
dfs(rt.right, rt) | |
} | |
dfs(root, null) | |
let vis = new Map() | |
let nowv = q | |
while (nowv) { | |
vis.set(nowv, true) | |
if(fa.has(nowv)) | |
nowv = fa.get(nowv) | |
} | |
nowv = p | |
while (nowv) { | |
if(vis.has(nowv)) | |
return nowv | |
if(fa.has(nowv)) | |
nowv = fa.get(nowv) | |
} | |
}; |
思路二则是利用二叉搜索树的性质,从根节点开始遍历,官方题解如下:
- 若当前节点值大于
p和q的值,说明p和q应该在当前节点的左子树,将当前节点移动到它的左子节点; - 若当前节点的值小于
p和q的值,说明p和q应该在当前节点的右子树,将当前节点移动到它的右子节点; - 若等于当前节点的值不满足上述两条要求,那么说明当前节点就是「分岔点」。此时,
p和q要么在当前节点的不同的子树中,要么其中一个就是当前节点。
/** | |
* @param {TreeNode} root | |
* @param {TreeNode} p | |
* @param {TreeNode} q | |
* @return {TreeNode} | |
*/ | |
var lowestCommonAncestor = function(root, p, q) { | |
if(!root) return null | |
if(root.val < p.val && root.val < q.val) | |
return lowestCommonAncestor(root.right, p, q) | |
else if(root.val > p.val && root.val > q.val) | |
return lowestCommonAncestor(root.left, p, q) | |
else return root | |
}; |
# 剑指 Offer 68 - II. 二叉树的最近公共祖先
给定一个二叉树,找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
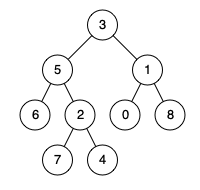
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
注意:本题与主站 236 题相同:https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/
# 思路与代码
用上题的思路 1 就好了。
fa 存每个结点的父节点,从上向下遍历一次初始化 fa ,再从下往上初始化 vis
var lowestCommonAncestor = function(root, p, q) { | |
if(!root) return null | |
let fa = new Map() | |
function dfs(rt, pre) { | |
if (rt === null) return | |
fa.set(rt, pre) | |
dfs(rt.left, rt) | |
dfs(rt.right, rt) | |
} | |
dfs(root, null) | |
let vis = new Map() | |
let nowv = q | |
while (nowv) { | |
vis.set(nowv, true) | |
if(fa.has(nowv)) | |
nowv = fa.get(nowv) | |
} | |
nowv = p | |
while (nowv) { | |
if(vis.has(nowv)) | |
return nowv | |
if(fa.has(nowv)) | |
nowv = fa.get(nowv) | |
} | |
}; |
