本章以几个典型对称密码算法为例，介绍对称密码算法实现过程、机理及特点，理解密码算法的应用背景。

内容概述

Chapter-4: 对称密码技术

本章以几个典型对称密码算法为例，介绍对称密码算法实现过程、机理及特点，理解密码算法的应用背景。

几个经典的古典密码方案
数据加密标准 DES
高级加密标准 AES
流密码算法
分组密码算法工作模式

# 古典密码

古典密码主要分为两种：置换密码与代换密码

# 置换密码

置换密码的特点是保持明文的所有字符不变，只是利用置换打乱了明文字符的位置和次序。也就是改变了明文的结构，不改变明文内容

通过改变明文字符的位置来实现加解密
典型：栅栏密码、行移位密码等

# 代换密码

将明文字母替换成其他字母、数字或符号的方法
如果把明文看成是 0 或 1 的比特序列，那么密文就是 0 或 1 比特序列的另一种表达。简单粗暴
典型：凯撒密码

# 凯撒密码

所知道的最早的代替密码
由 Julius Caesar 发明，首先用在军事通信中
基本思想：通过将字母移动一定的位数实现加解密
eg: 每个字母用其后的第三个字母代替（也称 移位密码）

明文	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o	p	q	r	s	t	u	v	w	x	y	z
密文	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z	A	B	C

加解密方式 1：查表👆

加密方式 2：公式计算

编码明文： $a=0,b=1,…,z=25$ ，则明文 $P=p1p2…pn$
加密运算： $c_i=p_i+k \bmod 26,i=1,2,…,n$ ，
得密文： $C=c_1c_2…c_n$

解密方式 2：公式计算

密文： $C=c_1c_2…c_n$
解密运算： $p_i=c_i-k \bmod 26,i=1,2,…,n$ ，
解密得明文： $P=p_1p_2…p_n$

也即凯撒密码的加解密算法如下：

加密算法： $c = E(p) = (p+k) \bmod (26)$
解密算法： $p = D(c) = (c-k) \bmod (26)$

密码分析：

恺撒密码共有密钥 25 个
可简单地 依次去测试 ，穷举攻击
基于字母频率的破译方法
所破译的明文需要识别

eg：破译密文 "GCUA VQ DTGCM"

dzrx sn aqdzj( k=3 )
easy to break (k=2) 这不就出来了！

# 单表代换密码（代换 / 替换 / 代替）

可阅读博客：单表代换密码体制

特点：

不是简单有序地字母移位
可任意地打乱字母的顺序
每个明文字母映射到一个不同的随机密文字母
代换关系可以是一对多，但是必须要保证可逆性
密钥数目: 26! (26 的阶乘)

貌似很安全，但其实还是可以通过语言频率进行密码分析

人类的语言是有冗余的
字母的 使用频率 是不同的
如在英语中 E 使用的频率最高
有些字母使用较少
单字母、双字母、三字母组合统计

# 多表代换密码（维尼吉亚，Vigenere 密码）

多表代换密码跟单表代换密码的区别主要是：多表代换的代换表有多个。

对于加密，交替使用不同的代换表
字母的使用频率分布更加平坦
加密和解密所用的代换表顺序一致
典型例子就是：维尼吉亚密码

维吉尼亚密码是最简单的多表代换密码，由多个凯撒移位密码组成。其明文字符集为 a~z，26 个英文字母。将字母按顺序循环移位 k 个，形成一个代换表

维尼吉亚方阵如下：

维尼吉亚方阵

例如，假设明文为： ATTACKATDAWN

选择某一关键词并重复到与明文等长（过短则截取）而得到密钥，如关键词为 LEMON 时，密钥为： LEMONLEMONLE
对于明文的第一个字母 A ，对应密钥的第一个字母 L ，于是使用表格中 L 行字母表进行加密，得到密文第一个字母 L
类似地，明文第二个字母为 T ，使用表中对应的 E 行进行加密，得到密文第二个字母 X。以此类推，可以得到：

明文： ATTACKATDAWN
密钥： LEMONLEMONLE
密文： LXFOPVEFRNHR

解密的过程则与加密相反。

密钥第一个字母 L 对应 L 行字母表，发现密文第一个字母 L 位于 A 列，因而明文第一个字母为 A
密钥第二个字母 E 对应 E 行字母表，而密文第二个字母 X 位于此行 T 列，因而明文第二个字母为 T 。以此类推便可得到明文。

也即维吉尼亚密码的加解密算法如下：

加密算法： $c_i = E_{k_i}(p_i) = (p_i+k_i) \bmod 26$
解密算法： $p_i = D_{k_i}(c_i) = (c_i-k_i) \bmod 26$

可见 Vigenere 密码与单表代换密码的区别仅仅在于：单表移位密码中的位移量 k 是一个固定的常数；而 Vigenere 密码中的 ki 是变化的，字母的位置不同，则所采用的位移量也不同

加解密过程 js 代码如下：

	/*
	* @Author: cos
	* @Description: Vigenere 加密解密过程
	* @FilePath: \secure\exp_1\Vigenere.js
	*/
	class Vigenere {
	ascii; //ascii [i] 表示第 i 个字母的 ascii 码
	matrix;
	constructor() {
	this.ascii = new Array(26).fill(0).map((v, i) => String.fromCharCode(65+i))
	this.matrix = new Array(26).fill(0).map(() => new Array(26));
	for(let i = 0; i < 26; ++i)
	for(let j = 0; j < 26; ++j)
	this.matrix[i][j] = this.ascii[(i+j)%26]; // 列主密钥
	}
	// 根据明文和关键字生成密钥
	buildKey(plain, keyword) {
	let [len1, len2] = [plain.length, keyword.length]
	if(len1 <= len2) return keyword.substr(0, len1)
	let cnt = Math.floor(len1/len2)
	return keyword.repeat(cnt) + keyword.substr(0, len1-(len2*cnt));
	}
	// 根据明文 plain 和密钥关键词 keyword 进行加密
	encrypt(plain, keyword) {
	let capitalPlain = plain.toUpperCase(); // 注意先将密钥和明文转为大写
	let key = Vigenere.prototype.buildKey(capitalPlain, keyword.toUpperCase())
	let len = capitalPlain.length;
	let res = "";
	for(let i = 0; i < len; ++i) {
	let idx = key.charCodeAt(i)-65 // 选用第 idx 行的
	let jdx = capitalPlain.charCodeAt(i)-65
	let nowchar = this.matrix[idx][jdx]
	res += plain[i] <= 'Z' ? nowchar : nowchar.toLowerCase() // 若是小写，则密文也对应小写。
	}
	return res;
	}
	// 根据明文 plain 和密钥关键词 keyword 进行加密
	decrypt(encrypted, keyword) {
	let capitalEd = encrypted.toUpperCase(); // 注意先将密钥和明文转为大写
	let key = Vigenere.prototype.buildKey(capitalEd, keyword.toUpperCase())
	let len = capitalEd.length;
	let res = "";
	for(let i = 0; i < len; ++i) {
	let idx = key.charCodeAt(i)-65 // 选用第 idx 行的
	let jdx = this.matrix[idx].findIndex(v => v == capitalEd[i]); // 在该行中找到密文对应的 ascii 码
	let nowchar = this.ascii[jdx]
	res += encrypted[i] <= 'Z' ? nowchar : nowchar.toLowerCase() // 若是小写，则解密出来的字母也对应小写。
	}
	return res
	}
	printMatrix() {
	console.log("方阵如下：")
	for(let i = 0; i < 26; ++i)
	console.log(this.matrix[i].join(''))
	}
	}
	module.exports = new Vigenere();

主函数

	/*
	* @Author: cos
	* @Description: 主类
	* @FilePath: \secure\exp_1\Main.js
	*/
	// 测试函数
	const v = require('./Vigenere')
	function testCase(plain, keyword) {
	console.log(`明文为:${plain}, 密钥为:${keyword}`)
	let encrypted = v.encrypt(plain, keyword)
	console.log(`密文为:${encrypted}`)
	let decrypted = v.decrypt(encrypted, keyword);
	console.log(`解密得:${decrypted}`)
	}
	let testCases = [
	["ATTACKATDAWN", "LEMON"],
	["HelloWorld", "haoye"],
	["QwQqwqOVO", "WHXHP"],
	["BUS", "YELLO"],
	["abcdEFGhiJK", "NaHCOx"],
	["DidILoveU", "cos"],
	]
	for(let i = 0; i < testCases.length; ++i) {
	console.log(`----------------样例${i}----------------`)
	testCase(...testCases[i])
	}
	v.printMatrix()

输出结果：

其他典型多表代换密码有：希尔密码（Hill）、转轮密码等……

# 数据加密标准 DES

如何实现加解密过程相同、密钥相同的对称密码算法？

数据加密标准 DES (Data Encryption Standard) 是个著名分组加密算法。

美国国家标准局 1973 年 5 月公开征集用于计算机数据在传输和存储期间实现加密保护的密码算法。

1975 年美国国家标准局接受了 IBM 公司提交的一种密码算法并向社会公开征求意见。
1977 年正式采用该算法作为美国数据加密标准。
1980 年 12 月美国国家标准协会正式采用该算法作为美国商用加密算法。

美国国家标准局征求加密算法的要求：

提供高质量的数据保护，防止数据未经授权的泄露和未被察觉的修改。
具有相当高的复杂性，使得破译的开销超过可能获得的利益，同时又便于理解和掌握。
密码体制的安全性应该不依赖于算法的保密，其安全性仅以加密密钥的保密为基础。
实现经济，运行有效，并且适用于多种完全不同的应用。

# 概述

DES 是一种分组密码算法，加密和解密使用相同的密钥
DES 的分组长度为 64 比特位
使用 64 比特密钥（其中包括 8 比特奇偶校验位)，密钥通过扩展后产生 16 个子密钥。
经过 16 轮对明文分组的代换和置换
DES 算法的步骤，包括 IP 置换、密钥置换、E 扩展置换、S 盒代替、P 盒置换和逆初始置换 IP-1……（寄）

…… 后续视题型再补充！先看博客吧，感觉不会考具体步骤：数据加密算法 -- 详解 DES 加密算法原理与实现

加 / 解密密钥相同有何好处？用户只需记忆一个密钥，就可用于加密、解密。
加密解密的计算量小，速度快，简单易用，适合于对海量数据进行加密处理。
长度为什么选择 64 比特？可进行奇偶校验，每 8 位可以用于奇偶校验
密钥长度为 64 bit，但是实际数据长度只有 56 位，还有 8 位为奇偶校验位
校验码这一块推荐 3B1B 的视频：【官方双语】汉明码 part2，优雅的全貌

# 高级加密标准 AES

如何设计数学上可证明安全性的对称密码算法？

1997.4.15，NIST 发起征集高级加密标准的活动，目的是确定一个可以公开技术细节的、全球免费使用的分组密码算法，作为新的数据加密标准。

1997.9.12，美国联邦登记处公布了正式征集 AES 候选算法的通告。作为进入 AES 候选过程的一个条件，开发者承诺放弃被选中算法的知识产权。

NTST 对 AES 算法的要求：

算法应比三重 DES 快，而且至少还要一样的安全
应具有 128 比特分组长度和 128/192/256 比特密钥长度

64 比特密钥已经能够破解

1998.8.12 首届 AES 会议 NIST 收到 15 个候选算法。1999.3.22 第二次 AES 会议将候选名单减少为 5 个:

MARS (IBM)、RC6 (MIT)、Rijndael（比）、 Serpent (英、以、美)、Twofish（美)

2000.4.13 第三次 AES 会议上，对这 5 个候选算法的各种分析结果进行了讨论。

2000.10.2，NIST 宣布了获胜者:

比利时密码专家 Vincent Rijmen 和 Joan Daemen 设计的 Rijndael 算法

2001 年 11 月出版了最终标准 FIPS PUB197，该算法称为 AES: Advanced Encryption Standard .

# Rijndael 算法

分组长度为 128 比特，密钥长度为 128/192/256 比特
使用 替换置换网络 设计，而没有采用 Feistel 结构，软硬件实现都很快。
基本特性
- 能够抵抗已知的所有攻击
- 在各种平台上执行速度快，代码紧凑
- 设计简单

# AES 基本操作流程

AES 由多轮操作组成，轮数由 分组和密钥长度 决定。

AES 在 4×n 字节的数组（矩阵）上操作，称为状态 (State)，其中 n 是密钥字节数除 4。

AES 的数据结构

以字节为单位的方阵描述：输入分组 in 、中间数组 State 、输出分组 out 、密钥分组 K
排列顺序：方阵中数据从上到下，从左到右排开

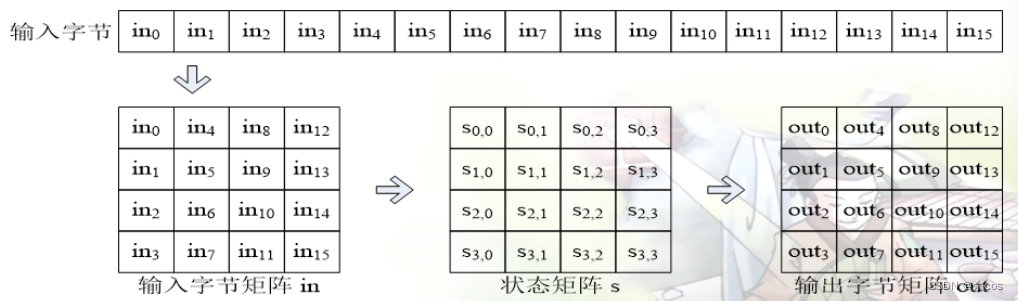
在这里插入图片描述

允许分组和密钥以 128 比特为基础，以 8 字节倍数扩展长度
- 因此 192、256 比特分组或密钥被组织成 4×6、4×8 矩阵
AES 标准中使用 $N_b$ $N_{b}$ 、 $N_k$ $N_{k}$ 分别表示分组矩阵、密钥矩阵列数
- 如当分组为 4×6 矩阵， $N_b=6$ ，密钥为 4×8 矩阵，则 $N_k=8$
AES 算法流程中轮数依赖于密钥长度，标准中使用 $N_r$ 表示轮数。
AES 包括 3 个分组密码套件：AES-128、AES-192、AES-256，对应 $N_k$ 分别为 4、6、8，密钥长度对应 128、192 和 256 比特，对应轮数 $N_r$ 等于 10、12、14，分组长度都为 128 比特

此处省略亿堆操作具体流程：AES 加密算法的详细介绍与实现

其他分组密码算法： IDEA 算法、 Blowfish 算法、 RC5/RC6 算法

# 流密码算法 RC4

如何实现 “无限” 长度密钥的对称密码算法？

主密钥：通信双方共享的一定长度密钥

RC4 算法

由主密钥按一定密钥调度算法 产生任意长度伪随机密钥字节流 (以字节为单位)
与明文流 按字节异或 生成密文流
解密时密文流与 相同的密钥流同样按字节异或 恢复出明文字节流。

好，对称加密之流密码 RC4

# 分组密码工作模式

电子密码本（ECB：Electronic Code Book）模式
密文分组链接（CBC：Cipher Block Chaining）模式
密文反馈（CFB：Cipher-FeedBack）模式
输出反馈（OFB：Output-FeedBack）模式
计数器（CTR：Counter mode）模式

信息安全概论